Face Morphing
Part of CS180 : Intro to Computer Vision and Computational Photography
In this project, I will explore the process of face morphing and transforming one face into another using advanced image manipulation techniques. I will cover key concepts such as correspondence, triangulation, and interpolation, and show how they work together to create smooth transitions between images. Additionally, I generate average faces for groups, create caricatures by exaggerating features, and apply dimensionality reduction techniques like PCA to facial data.
Through this project, I will demonstrate not only how face morphing works but also how these techniques can be used to visualize population averages and highlight distinctive facial features.
Correspondence
A key element of successful face morphing is establishing accurate correspondence points between two images. These points define the landmarks on the face that will be matched and blended between images, ensuring the facial features align smoothly as we transition from one face to another.
For this project, I selected the following key regions for correspondence:
- Eyes (8 points) – The eyes are central to human recognition and expression, so placing multiple points around them helps capture their shape and position accurately, ensuring they transition smoothly during the morph.
- Eyebrows (8 points) – Eyebrows contribute significantly to facial expression. By marking key points around the eyebrow, we can preserve their subtle shifts in shape and position.
- Nose (7 points) – The nose is a prominent facial feature that anchors the center of the face. Correspondence points here help maintain the structural integrity of the face during the morph, especially across different face shapes.
- Mouth (4 points) – Points around the mouth capture its overall shape and width. As the mouth is highly expressive, it’s important for these points to align well to avoid distortion in expressions like smiles or neutral faces.
- Ears/Chin (11 points) – These points help define the contour of the face. The chin and jawline, in particular, vary significantly between individuals, so capturing these features accurately is crucial for realistic morphing.
- Forehead/Hairline (7 points) – Including points on the forehead and hairline helps ensure that the upper face and hair are also morphed consistently, preserving the overall face shape.
- Neck/Shoulders (6 points) – These points provide context for the head and its orientation, helping to avoid awkward transitions at the base of the neck and shoulders, which can distort the alignment.
- Top of Hair (7 points) – These points ensure that the hair, often a distinctive feature, blends well during the morph.
- Image Border (4 points) – Marking the image border provides stability during the transformation, keeping the morph consistent and preventing unwanted distortion at the edges of the images.
By carefully placing correspondence points on these regions, I encapsulate the key features that make each face unique. This approach ensures that the facial features people naturally focus on—eyes, nose, mouth, and jawline—are properly aligned, making the morph look natural and smooth.



Using these correspondence points, I apply Delaunay triangulation to divide the image into a network of triangles. Each triangle is then morphed individually from one image to the other, ensuring smooth transitions between corresponding facial features. To begin the process, I first compute the average positions of the points from both images and generate the Delaunay triangulation based on these average points. This provides a consistent structure for the morph, allowing each feature to blend seamlessly between the two images.

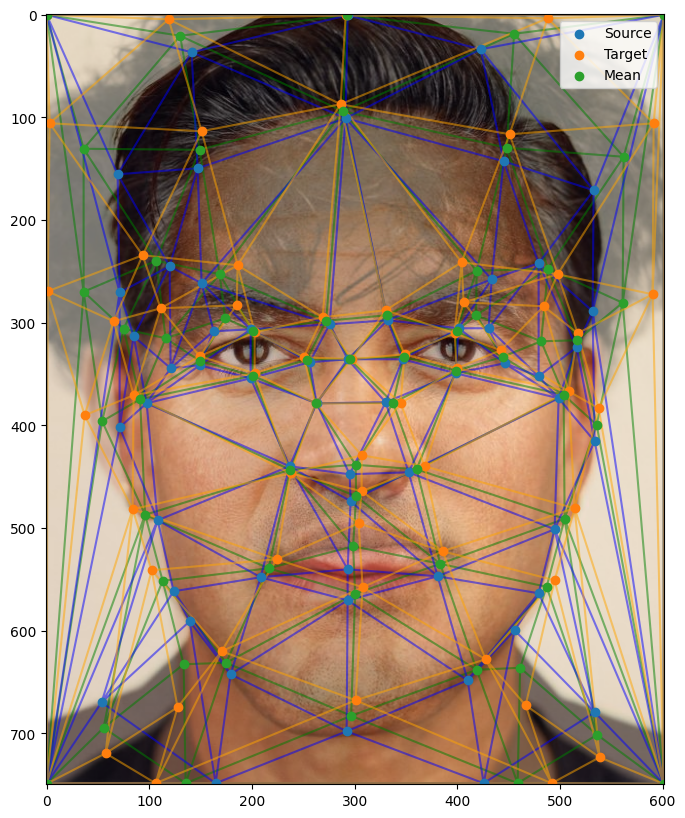
Midway Face
To morph between the two images, we begin by creating a “midway face.” This is done by warping the triangles from both original images into the shape of the triangles formed by the average points in the Delaunay triangulation. The midway face provides a balanced blend of the two faces, with the structure evenly aligned between them.
An important aspect of this process is using inverse warping rather than forward warping. In forward warping, each pixel in the source image is mapped to the target, which can leave gaps or “holes” in the morphed image due to rounding errors or insufficient coverage of the target pixels. In contrast, inverse warping ensures that every pixel in the target image is properly sampled from the source image. By mapping each pixel in the target back to the source, we avoid the issue of missing information and maintain a smooth, continuous appearance.
Additionally, to ensure high-quality results, we use an interpolator to sample the pixel values. Without interpolation, pixel sampling would be limited to discrete values, which can result in blocky, jagged edges or visual artifacts in the morphed image. The interpolator allows us to sample a continuous range of pixel values, smoothing the transition between different facial features and ensuring that the morph looks natural.


Morphing
To achieve the morph, I apply interpolation to produce a full range of intermediate points between the two images. The midway face was just one example, where the interpolation factor was set to 0.5. By varying this factor, I can generate a smooth transition from one image to the other, gradually morphing the facial features over a series of frames. For the point positions, a linear interpolator is used to create a continuous morph between the two sets of correspondence points, allowing the facial structure to change in a steady manner.
However, for color blending, I implement a sigmoid function to enhance the visual transition. The sigmoid function, mathematically represented as:
provides an S-shaped curve that allows for a rapid change in color around the midpoint of the morph when the two images are closely aligned. At the start and end of the morph, the sigmoid function ensures gentle transitions, preventing harsh changes in color and maintaining a natural appearance.
Overall, the use of inverse warping and a sigmoid function in the morphing process ensures that both the shape and color transitions between the images are smooth, continuous, and visually engaging.


Results
Results






Population Means
With this foundational knowledge, I can now compute the average face from a set of images. This process involves averaging the corresponding points across all the faces in the dataset, then morphing each individual face to align with this average. By calculating the average of these morphed faces, I can create visual representations of the average face for a population.
For this analysis, I utilized the IMM Face Database
The dataset categorizes facial expressions into several subtypes:
| Face Subtype | Description |
|---|---|
| 1 | Resting |
| 2 | Smile |
| 3 | Face Left |
| 4 | Face Right |
| 5 | Side Light |
| 6 | Variation |
Below are examples of the faces included in the dataset, showcasing the variety of expressions represented.
Dataset








I chose to divide the overall population into two groups based on the reported sex of the subjects in the dataset. This decision was informed by a comparative analysis of the average faces for each group, as well as the combined average face of both groups. I observed that the overall average face did not accurately represent the unique features of either group, prompting me to create distinct averages for a more nuanced representation.
Below are the resulting facial averages for the two groups, highlighting the differences and similarities in their features.




Here are some examples of members of the dataset morphed to the average face of their group.
Results

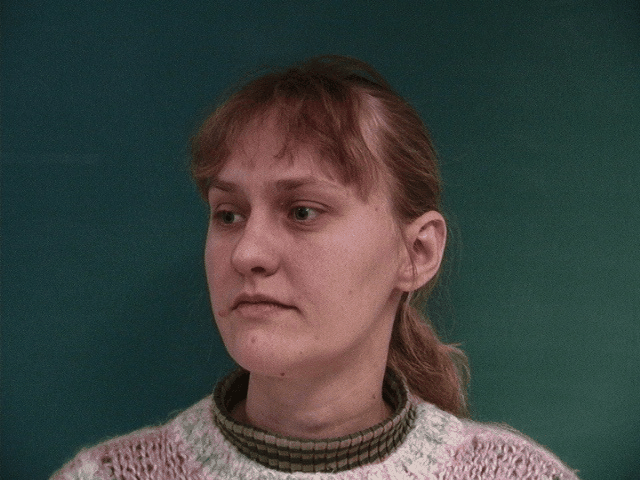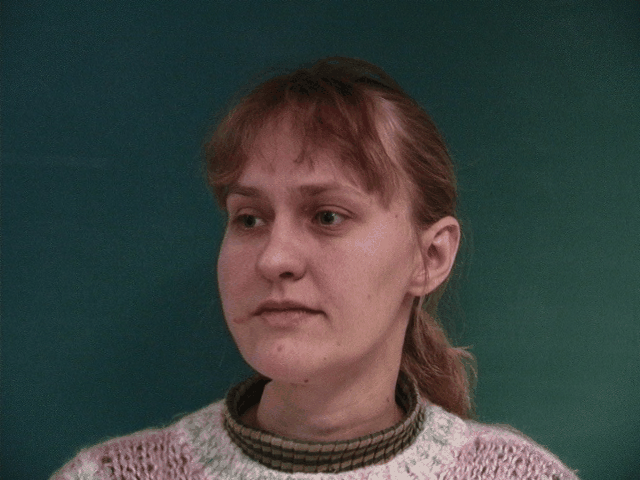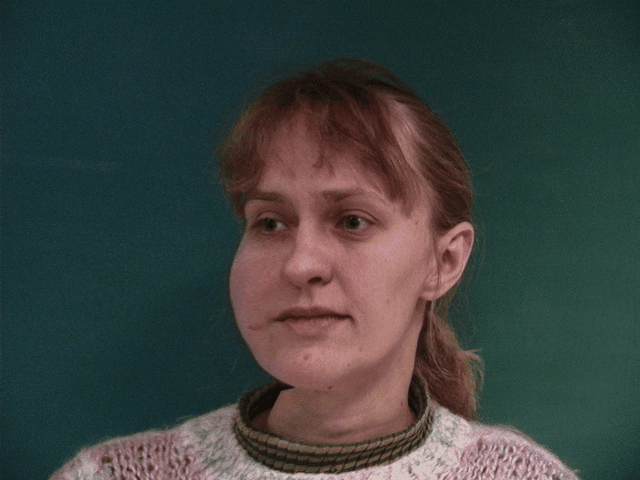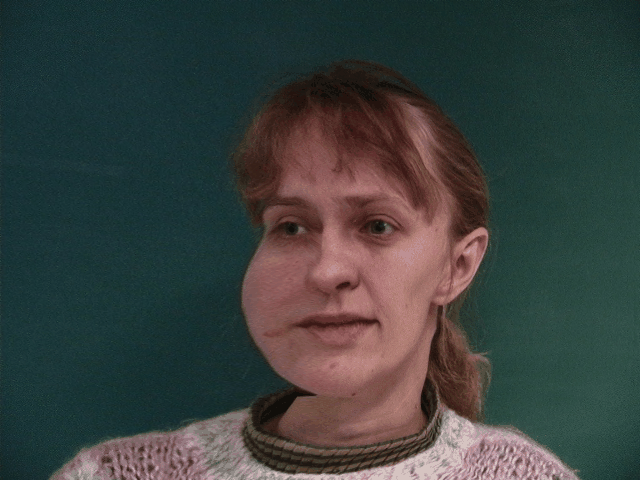
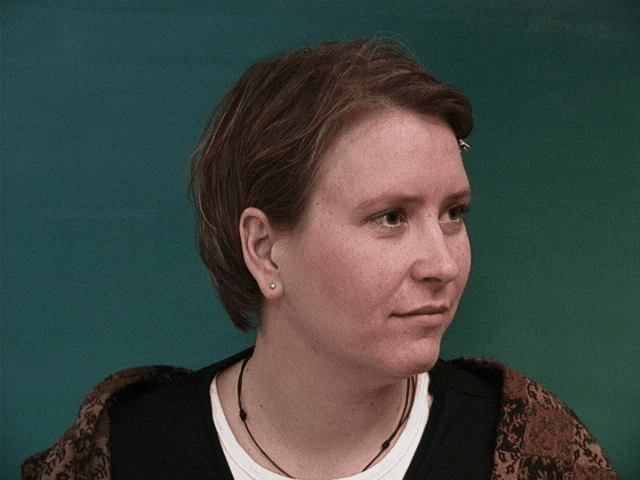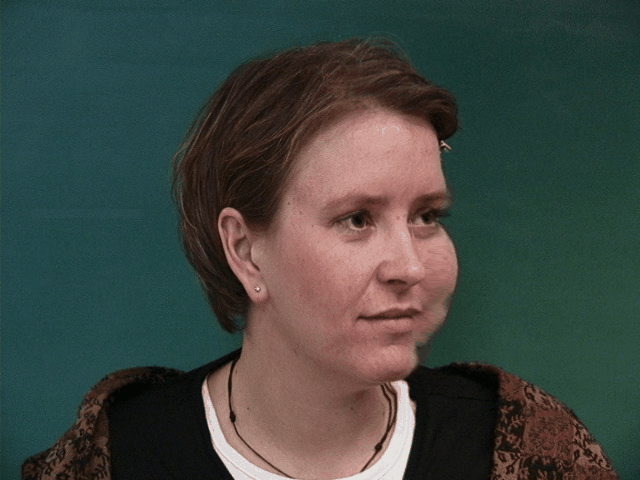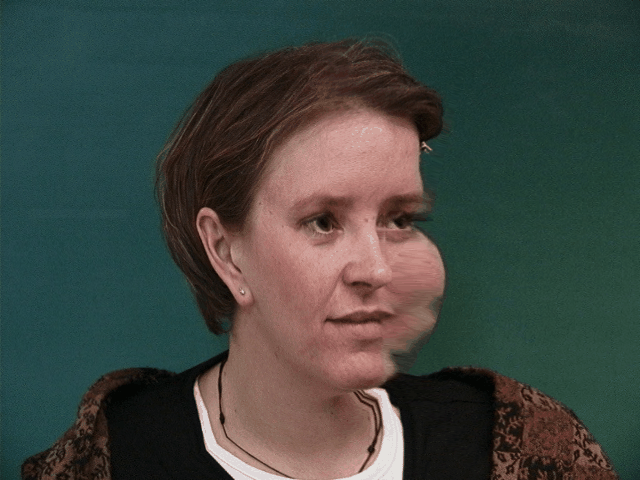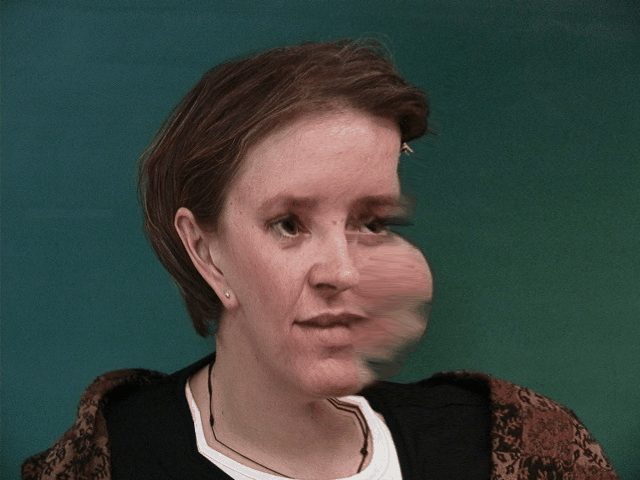







We can see some issues that arise from the choice of correspondence points in the image. The dataset uses points around the chin, eyes, eyebrow, mouth, and nose. It leaves out the ears, hair, and neck. This causes the morphing to be less accurate in these areas and produces smearing effects. This problem is most evident in the morphs from images where the subject is facing left or right. While the features of the face that are defined by the correspondence points are morphed correctly, the correspondence points do not contain information about overall facial orientation, so the rest of the face maintains the orientation of the original image, while the other features are morphed to the average face. This causes the face to appear to be twisted.
With the average faces and their corresponding points established, I can now morph these averages into new facial geometries to explore various representations. For this visualization, I will morph the average faces into the geometries of Sameer’s and my face.




Alternatively, we can reverse the process and morph our faces to align with the average points of the two groups.




The results of this morphing reveal a striking similarity between the two groups. This can be attributed to the fact that the average points for both groups are closely aligned, sharing many of the same key facial landmarks. Additionally, both averages exhibit a high degree of symmetry, contributing to the visual resemblance observed in the morphed faces.
Caricatures
Armed with the knowledge of morphing faces, I can extend this technique to other applications, such as creating caricatures. By extrapolating the points from the average face to a given individual, I can exaggerate specific facial features. This process involves scaling the points from the average face to align with the provided face and then morphing the original face to these newly adjusted points. The result is a stylized representation that emphasizes distinctive characteristics, resulting in a playful and exaggerated version of the original features.

In this extrapolation, the range from -1 to 0 corresponds to the movement of points from the average face toward the provided face, effectively capturing the transition between the two. Conversely, the range from 0 to 1 represents the further displacement of these points, moving them further away from the provided face’s points and average face’s points. With a larger extrapolation factor, the caricatured face exhibits exaggerated features, emphasizing the unique characteristics of the individual as compared to the average face from the dataset.
Bells and Whistles
Principal Component Analysis (PCA) is a powerful technique for reducing the dimensionality of datasets, allowing for a more compact representation of data. In this context, I applied PCA to the correspondence points of the faces as well as their color values. This dimensionality reduction can help streamline the data and facilitate further modifications to the faces.
However, my attempts to utilize PCA on the color representation of the faces yielded limited success. Although I successfully reduced the dimensionality of the color values, the resulting modifications to the faces were not satisfactory. The quality of the reproductions was poor, making the faces difficult to recognize. This challenge was exacerbated by the lack of diversity in the dataset, which hindered my ability to create an accurate representation of my own features. Consequently, I found it necessary to include my roommate’s face in the dataset to enhance the variety and improve the results. Additionally, I had to limit the subtypes of the faces to exclude the side lighting and variation expressions, as these images were causing the results to be less accurate.
Subject 35 - PCA Color Modifications


























Subject 41 (Naman) - PCA Color Modifications


























Subject 42 (Sameer) - PCA Color Modifications


























Component 1 seemed to cover the greyscale images as well as the shirt brightness, 2 focused on background lighting, and 3 focused on face direction. The rest of the components seemed to change the colors, but not in any way that was clearly interpretable.
Here are the eigenfaces for the color representation of the faces:

In contrast, applying PCA to the point representation of the faces yielded much more interpretable results. This approach allowed me to gain a clearer understanding of how each PCA component influenced the facial structures while maintaining the recognizability of the faces. The following section showcases the results of applying PCA to the point representations of the three subjects, highlighting the meaningful variations and features captured through this dimensionality reduction process. I was able to use all face subtypes to generate the PCA components, which allowed me to visualize the variations in the facial structures across the entire population of faces. In fact, I believe one of the top components captured the expression of a wink!
Subject 35 - PCA Point Modifications


























Subject 41 (Naman) - PCA Point Modifications


























Subject 42 (Sameer) - PCA Point Modifications


























The components seem to focus around the framing of the individual for the first 5 components, focusing on orientation, direction faced, position in frame, and the distance to the camera. The next 5 components varied the facial features, such as enlongating facial features, or mouth positioning. Remarkably, component 8 seemed to capture smiling and frowning, while component 9 captured winking.
In conclusion, while the application of PCA to color representations proved to be less effective for creating caricatures, the use of PCA on the point representations of faces demonstrated significant utility. This approach enabled me to manipulate facial features in a controllable and interpretable manner.