Rasterizer
Part of CS184 : Foundations of Computer Graphics
https://satish.dev/projects/homework_1/
In this project, I will explore the process of implementing rasterization, a fundamental technique in computer graphics that involves converting vector graphics into raster images.
Drawing Single Color Triangles
In my implementation I have devised two ways of rasterizing triangles given their points. The first method uses cross products to check if a given point is on a certain side of a triangle, and if it is on the same side for all 3 lines, we can confidently say that it is inside the triangle. The second method uses barycentric coordinates, and calculates the point’s validity using vectors along two sides of the triangle from the origin. I find the bounding box of the triangle using the minimum and maximum of it’s coordinates, then loop over that region and check all points in this bounding box.
To rasterize a triangle, my algorithm creates the smallest rectangle around the triangle by getting the minimum and maximum x and y. It then checks every point within this triangle via a double for loop to check whether it is inside the triangle or not. This algorithm is faster than checking every pixel in the entire image, but it cannot never be slower than checking every sample as there are no additional samples it is considering. My other attempts included a walk, however I was unable to get it to work on all cases, however I saw negligible performance improvements in the working cases.
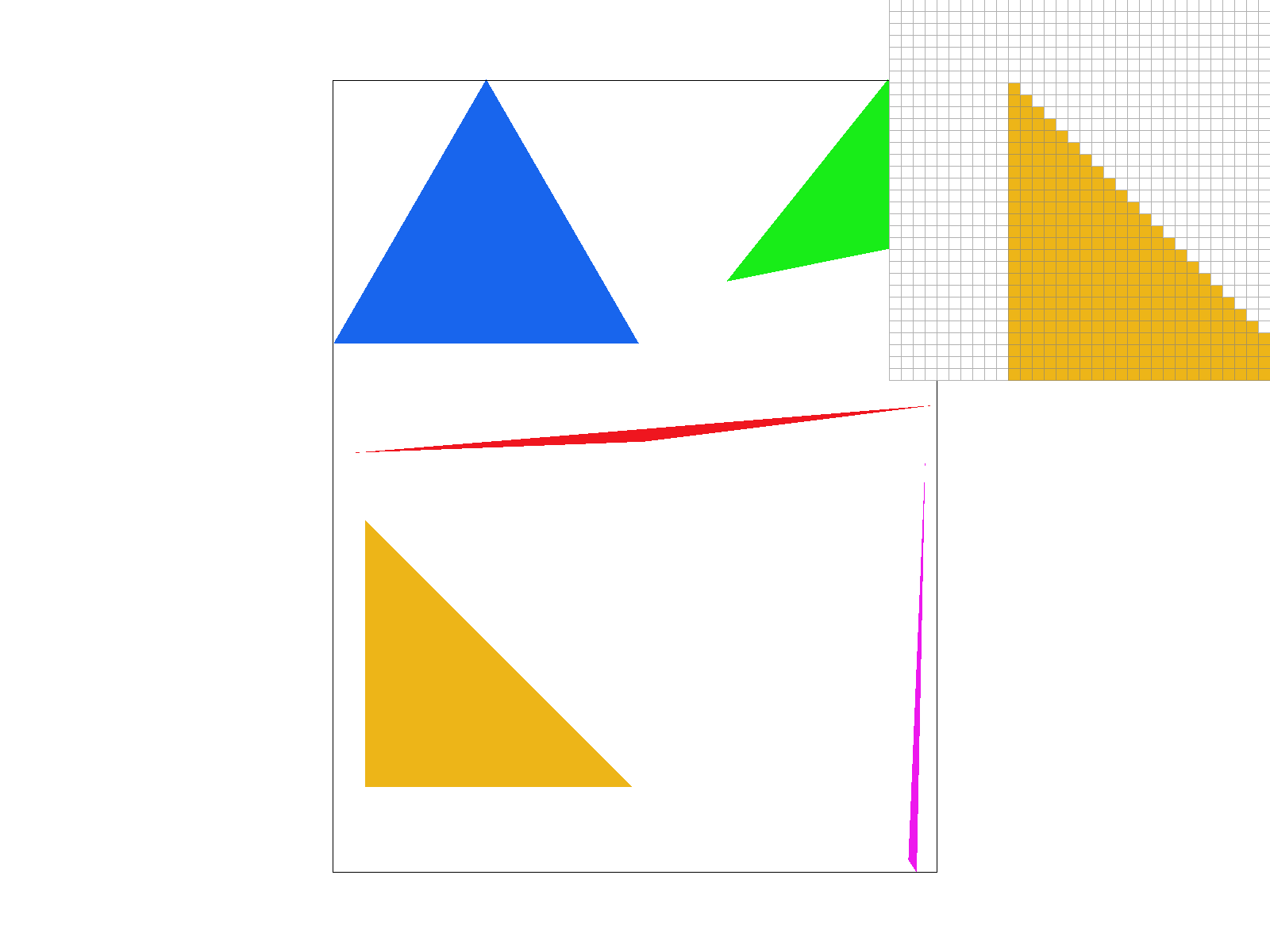
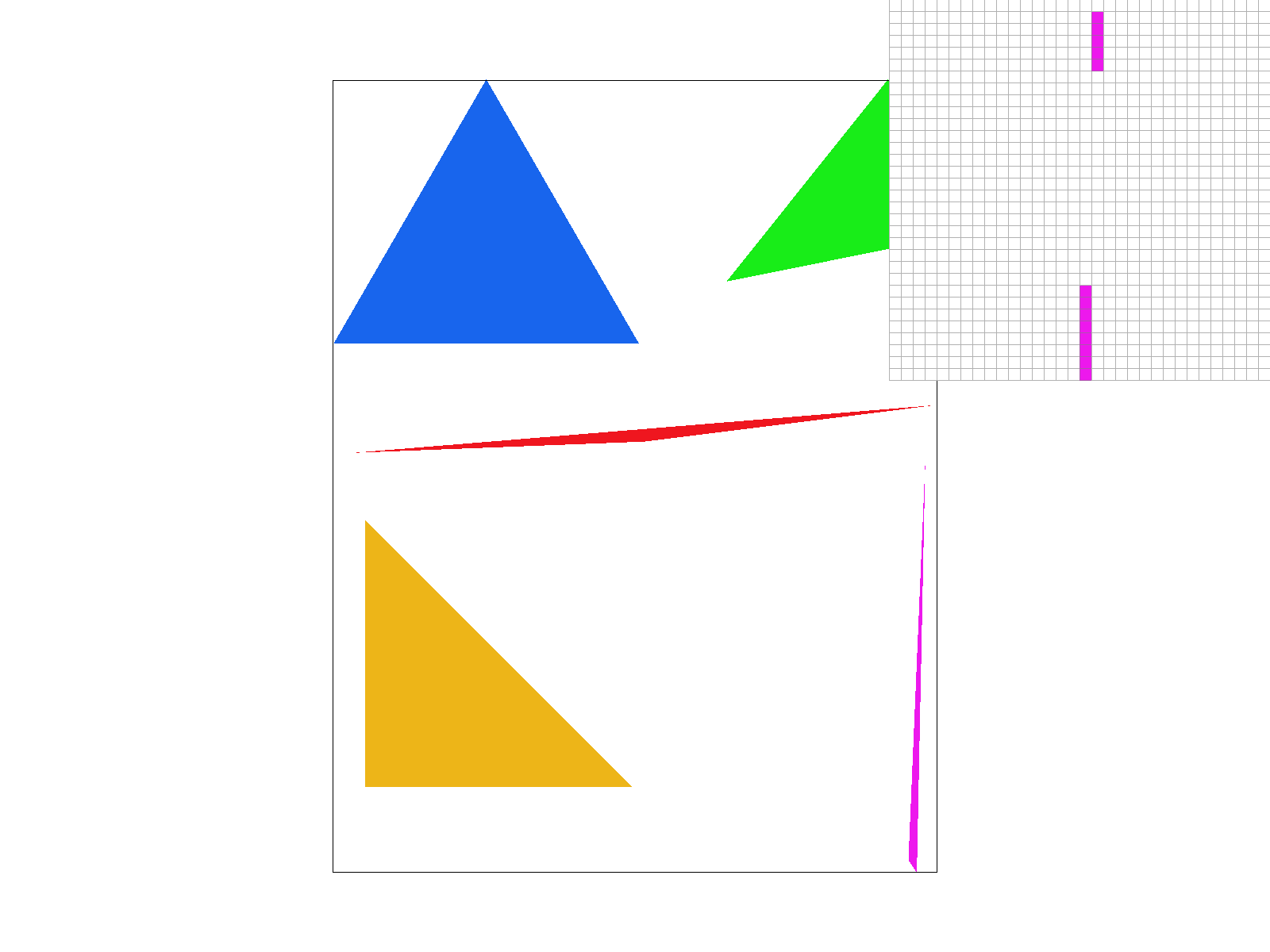
Antialiasing via Supersampling
As seen in the second example, there are issues with this simple approach as skinny edges can dissapear or appear jagged. To fix this, I implemented supersampling, which involves sampling multiple points within a pixel and averaging the colors to get a more accurate representation of the pixel. In my supersampling implementation, I kept a higher-resolution framebuffer called sample_buffer where each pixel was represented by multiple subpixels. This was achieved using an array with the dimensions of my original frame buffer, multiplied by the sampling rate.
The algorithm is as follows: I determine whether a subpixel was inside a triangle using one of my inside triangle functions, and if so I store the corresponding color value inside that subpixel. Once all triangles were rasterized, and all the subpixel sampling had concluded, I modified the logic in our conversion of our sample_buffer into the framebuffer by averaging the subpixel values within each pixel to generate the final color. This downsamples our higher resolution rasterization to the original resolution. Supersampling is useful because it enables the rasterization to turn jagged edges into slowly fading colors at boundaries rather than making abrupt transitions. For example, thin edges which may have had disconnected parts are now connected with supersampling. ing each feature to blend seamlessly between the two images.
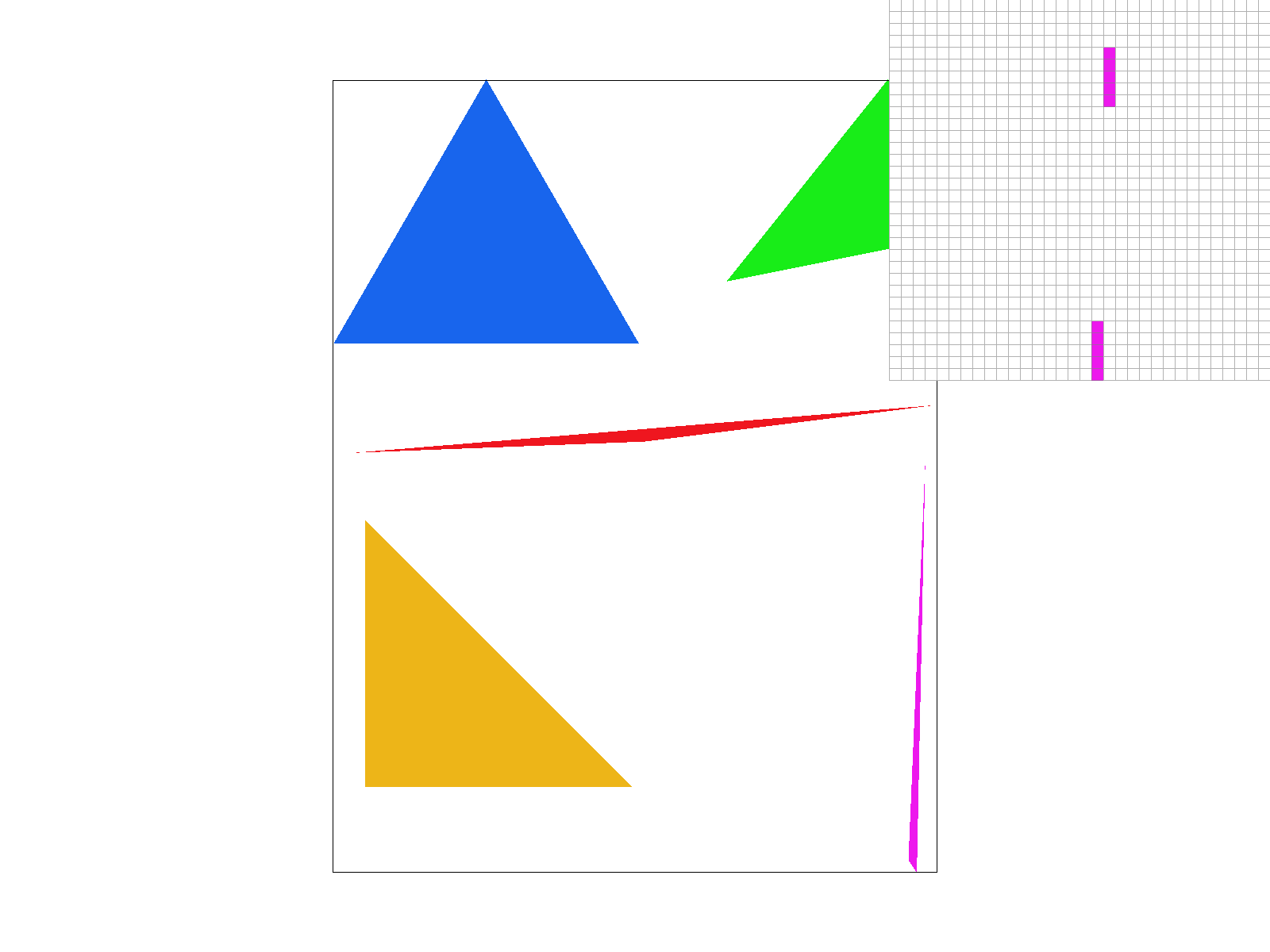
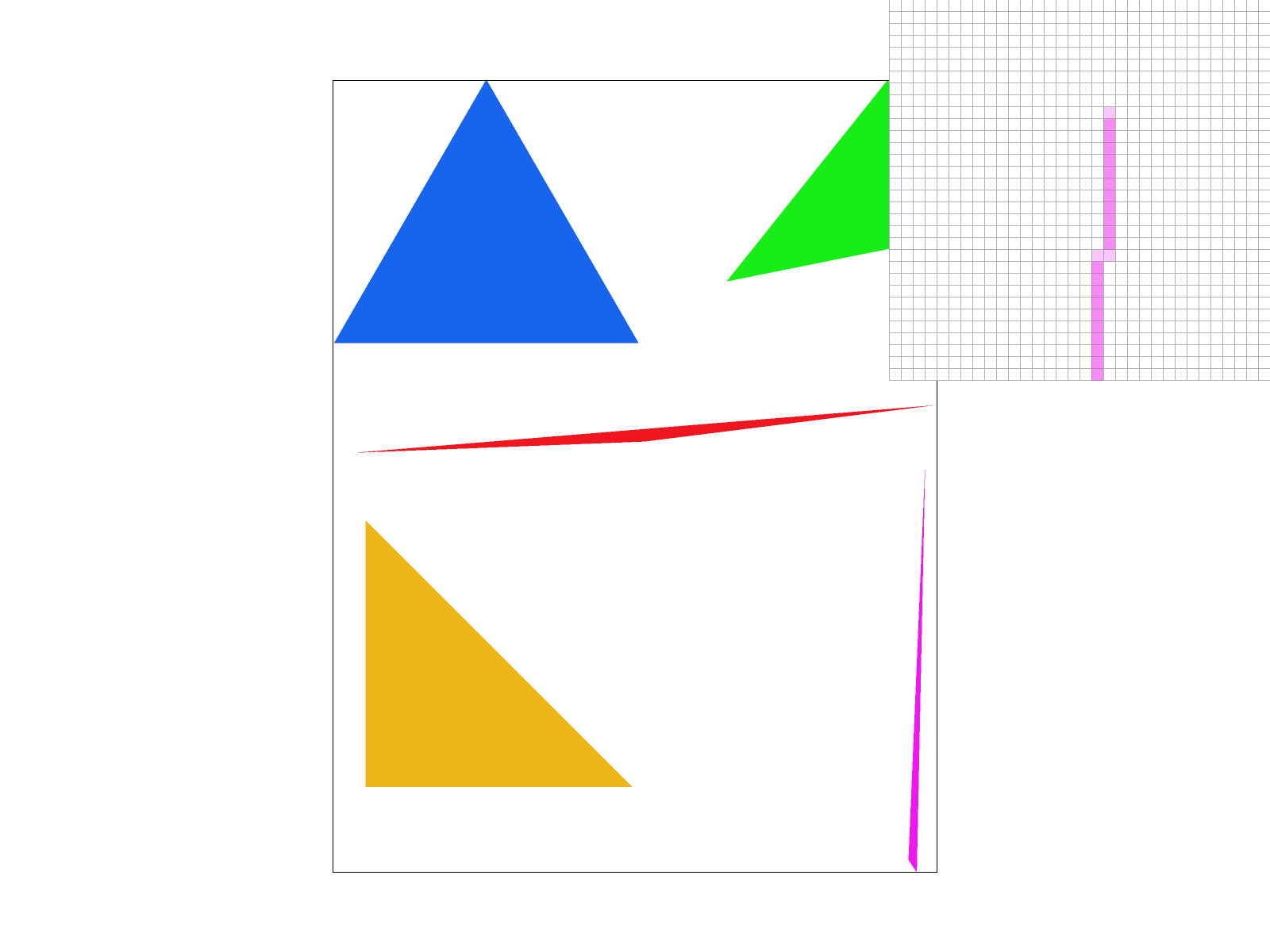
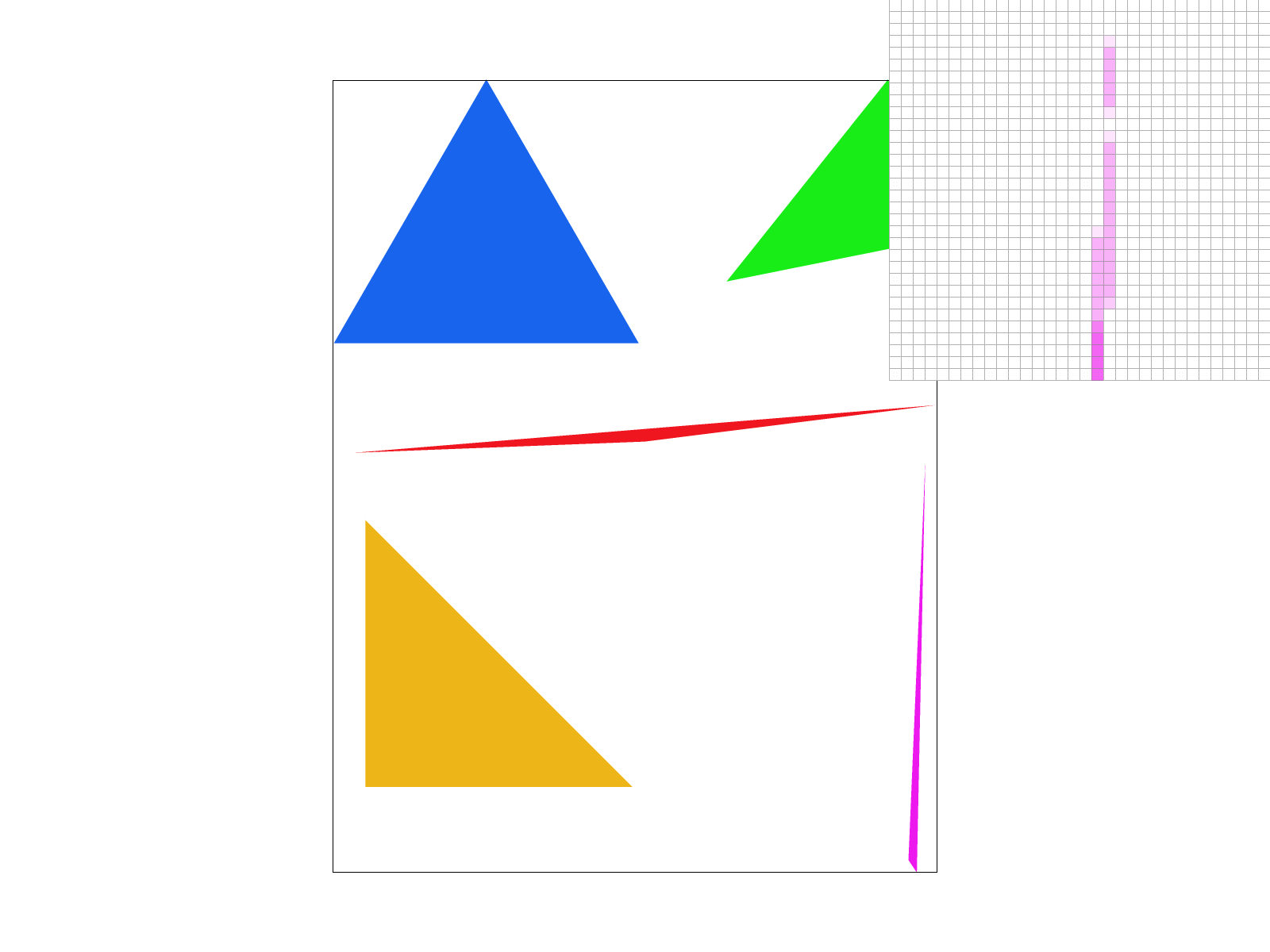
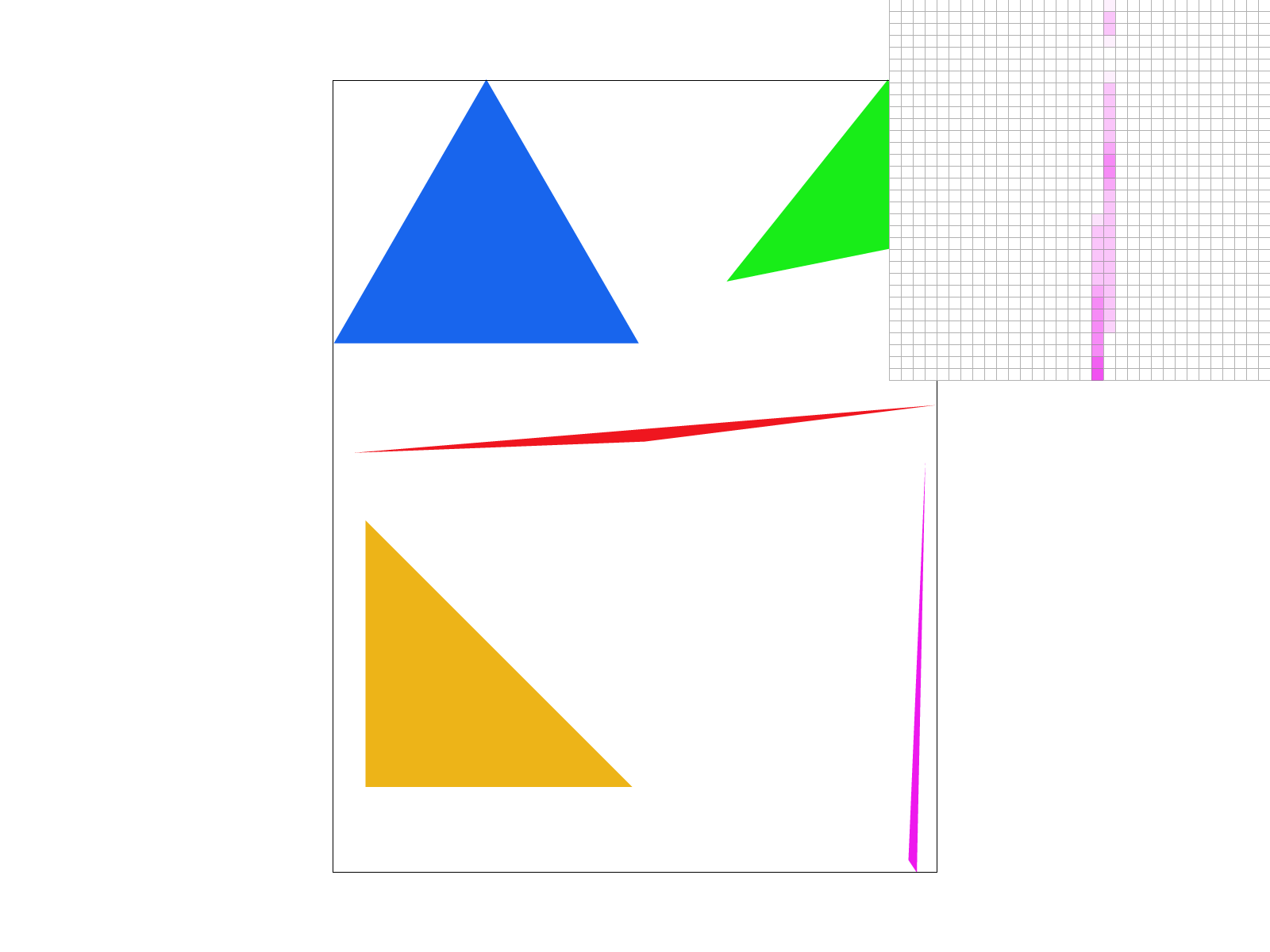
We can see that at higher supersampling the edge of the skinny triangle is not jagged and sharply defined, but expresses the nature of a tapering edge. This is more visually appealing as we don’t see disconnected parts of the same triangle, and see a smooth edge.
As we can see, the issue of separated edges is resolved with 4x supersampling, the edge of the skinny triangle is not jagged and sharply defined, but expresses the nature of a tapering edge. While the images may appear more visually appealing at higher sampling rates, and at a distance we see a smooth edge, our performance is worse and some disconnected edges may reappear as the majority of the sampling points fall outside the triangle.
Transforms
With transforms, we can rotate, scale, and translate our triangles. To do this, I implemented functions that created the corresponding transformation matrix for each operation. These matrices can be applied to the vertices in the order defined by the svg file to move triangles. In my case, I created a cubeman with his hands in the air as if he was about to catch a ball. So I gave him a colored team uniform, realistic skin, and positioned his hands up to catch and his legs as if he was running to where the ball was going to land.

Barycentric Coordinates
Barycentric coordinates are a method used to describe a point inside a triangle using the weighted sum of the triangle’s vertices. Since each triangle is defined by 3 vertices, each point in the frame is defined by 3 barycentric coordinates. These coordinates follow the property that points within the triangle have their sum of coordinates equal to 1. By computing 2 of the coordinates, we can get our third by subtracting 1. When a point is closer to a vertex, its corresponding barycentric coordinate will be higher and closer to 1, so we can use these coordinates to create a weighted average of the vertex colors to create smooth transitions! As we can see in the image, the further we get from red, to green and blue, the color begins to change, and in the center we get grey, the average of all 3 colors! 0.33,0.33,0.33 in RGB.


Pixel Sampling for Texture Mapping
Pixel sampling is the process of getting the correct color to apply to a pixel based on the corresponding texture for it. Within the triangle we assign texture coordinates to its vertices and can interpolate through these values to know where to fetch the color for a pixel in the triangle from. There are many considerations to take such as the shape of the pixel in texture space, and the challenges that occur with sampling. The two methods we implemented were Nearest and Bilinear. In nearest, we calculated the closest valid texcoord for our pixel, and then we get the value of this texel to apply to our pixel. In Bilinear, we get the 4 closest valid texcoords and use linear interpolation between all 4 texel values and the corresponding distances to produce an interpolated result.




We can easily compare the nearest 1x and bilinear 1x to see the stark difference in the readability of the letter B. The thin lettering caused by nearest sampling makes it difficult to understand what letter it is outside of context, however, in the bilinear example, the lettering is made much easier and is not as thin so we can more easily read the letter B even though it is very deformed. We will not see a big difference when our screen coordinates are very closely 1-1 defined with the textures, as the effects of bilinear sampling will be very minute and identical to nearest sampling. The difference will be great when the sampling is occurring at a different frequency, perhaps double that of the texture in a magnified case, as our bilinear will provide a smoother transition between the texels as compared to nearest which will be duplicating texels across multiple pixels. The effect is not as pronounced in the 16x sampling as the texels are closer to the screen coordinates, and the bilinear and nearest sampling will be very similar. This is because the section I chose is minified, supersampling using nearest will reach new texels and average them out, being comparable to the bilinear interpolation between the texels.
Level Sampling for Texture Mapping
Level sampling is a way to try and avoid aliasing by sampling from a texture that has the LOD (level of detail). For example, very compressed textures(ones that appear far away from the camera’s perspective) would sample from a blurry texture that would not cause aliasing to appear. This is because at the full texture, high frequency details would exceed the Nyquist frequency of the texture causing aliasing. We call these precomputed textures mipmaps, and because each is half the resolution of the prior, it only adds 25% to the total storage cost. To know what level we want to use, we calculate the x and y change in the texture space and scale to our 0th level. Then we use this to inform us what level we want to use after performing a norm operation and log2.






In my image of the Firefalls in Yosemite, you can see how the aliasing of the texture of the rocks is apparent and goes away with more applied to remove the aliasing. You can also see how personal preferences may differ in the use of aliasing, as it may conflict with the artistic intent of the image, sometimes jaggies are useful in showing the texture of the rocks.
Let us compare our options we have to modify our rasterization pipeline now!
Pixel Sampling : Nearest vs. Bilinear Filtering
| Factor | Nearest Sampling (P_NEAREST) | Bilinear Sampling (P_LINEAR) |
|---|---|---|
| Speed | Fastest (1 lookup) | Slower (4 lookups + LERP) |
| Memory | Constant | Constant |
| Anti-Aliasing | Bad (jagged edges, blocky appearance) | Better (smoother texture transitions) |
Level Sampling (LSM: Mipmaps)
| Factor | L_ZERO (No Mipmaps) | L_NEAREST (Discrete Mipmaps) | L_LINEAR (Trilinear) |
|---|---|---|---|
| Speed | Slowest (using full res, no ops) | Faster (1 mipmap lookup, no ops) | Medium (2 mipmap lookups + LERP) |
| Memory | Low (only one texture level) | 25% increase via Mipmaps | 25% increase via Mipmaps |
| Anti-Aliasing | Bad (has aliasing) | Good (reduces some aliasing) | Best (smoothest transitions) |
Supersampling (Samples Per Pixel)
| Factor | 1 Sample (Basic) | 4 Samples (Medium) | 9 Samples (Med High) | 16 Samples (High) |
|---|---|---|---|---|
| Speed | Fast | Slower (4x samples per pixel) | Slow (9x samples per pixel) | Slowest (16x samples per pixel) |
| Memory | Low | Medium (higher sample buffer size) | High (large buffer usage) | Highest (Exponentially growing) |
| Anti-Aliasing | Bad, Jagged | Good (smoother edges) | Better (still contains center pixel) | Debatable (Missing center pixel, most smooth) |
Final Tradeoff Summary
| Sampling Type | Speed | Memory Usage | Anti-Aliasing Quality |
|---|---|---|---|
| Pixel Sampling (PSM) | Fast | Low | Moderate |
| Level Sampling (LSM) | Fast (mipmaps) | Medium (25% increase) | Good (w/ trilinear) |
| Supersampling (Per Pixel) | Slowest | Exponentially Growing | Most accurate |