Bezier Curves and Triangle Meshes
Part of CS184 : Foundations of Computer Graphics
https://satish.dev/projects/homework_2
Overview
In this project, I implemented various algorithms for working with Bézier curves and triangle meshes. I started by implementing the de Casteljau algorithm for evaluating Bézier curves, which recursively interpolates between control points to compute the curve point at a given parameter. I then extended this algorithm to Bézier surfaces, which are defined by a grid of control points. I also implemented area-weighted vertex normals for shading, edge flip and split operations for mesh processing, and loop subdivision for mesh upsampling.
I began by understanding the underlying mathematics of Bézier curves which let me build up to Bézier surfaces. However, the challenge in understanding on how to effectively modify the mesh led to the need for the triangle mesh. This subsequently led to the implementation of area-weighted vertex normals to create smoother shading. In an attempt to regain the smooth parametric nature of the Bézier curves, I implemented the edge flip and split operations. However, by themselves, these operations could not be manually used to smooth out the entire mesh at once. This led to the implementation of loop subdivision, which allowed me to upsample the mesh and create a smoother mesh.
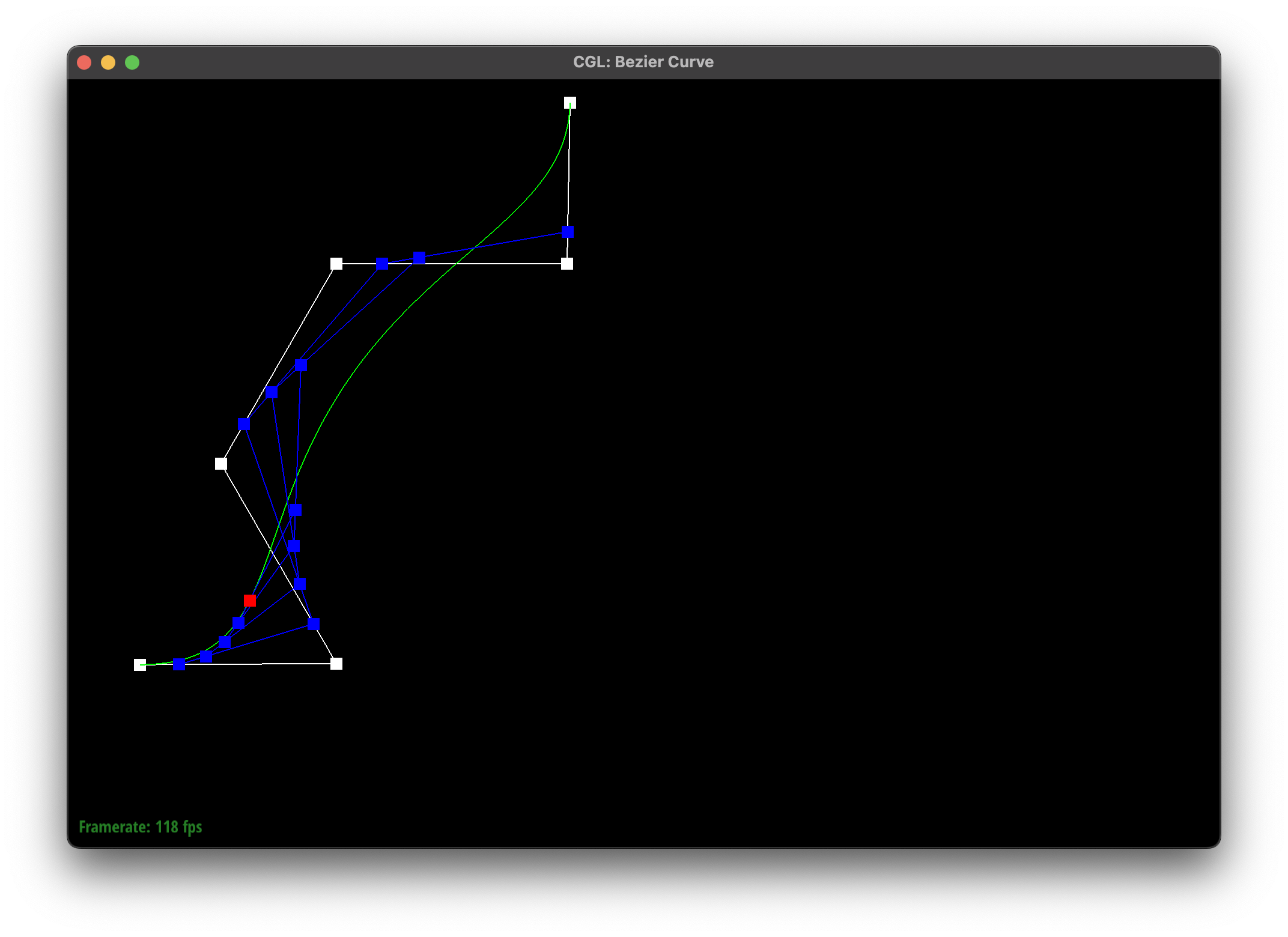
Bézier Curves with 1D de Casteljau Subdivision
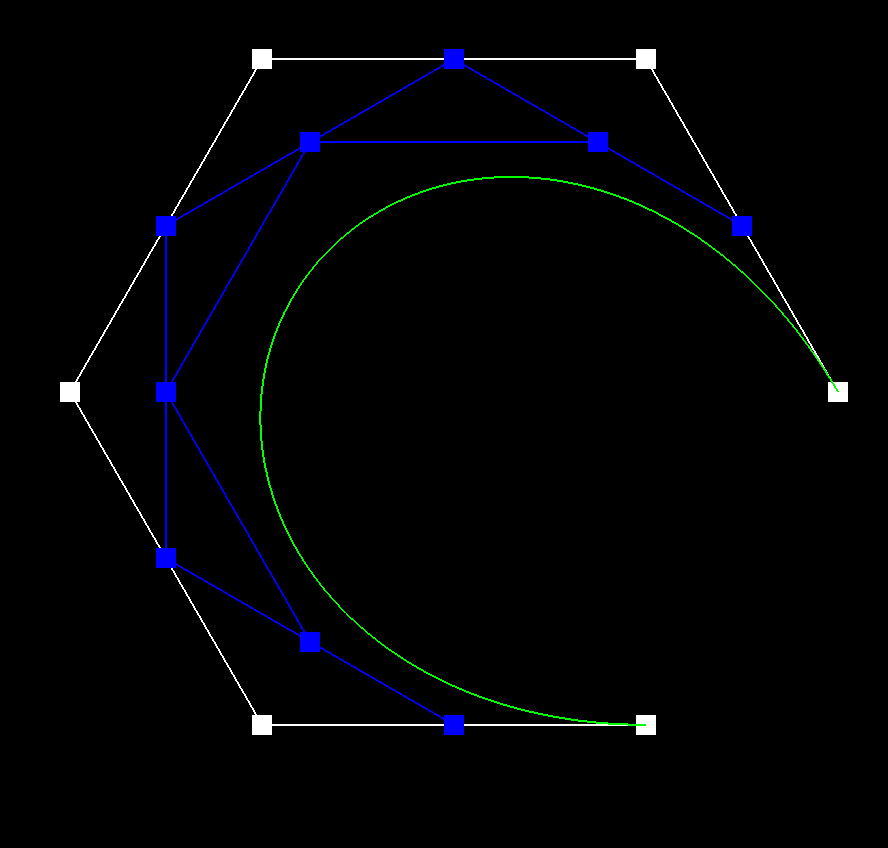
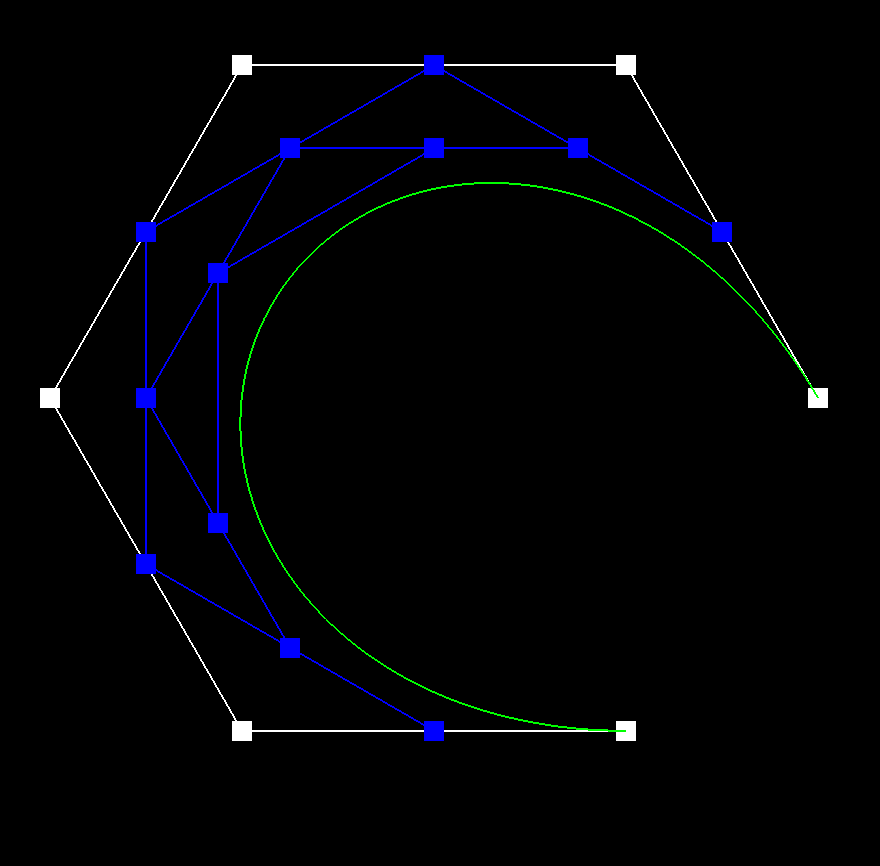
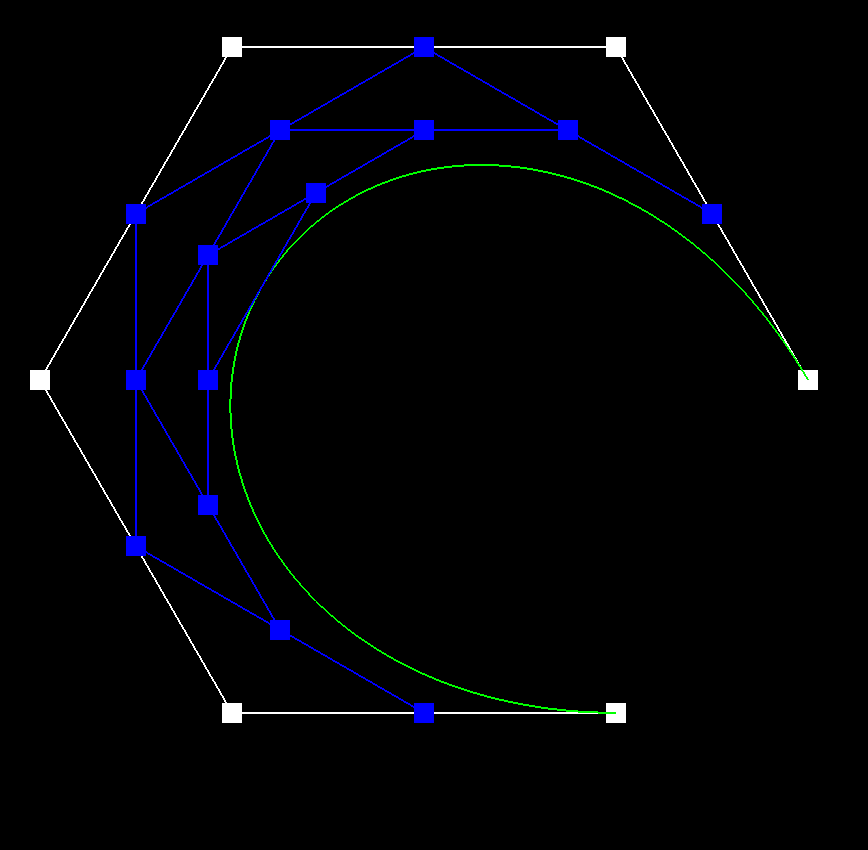
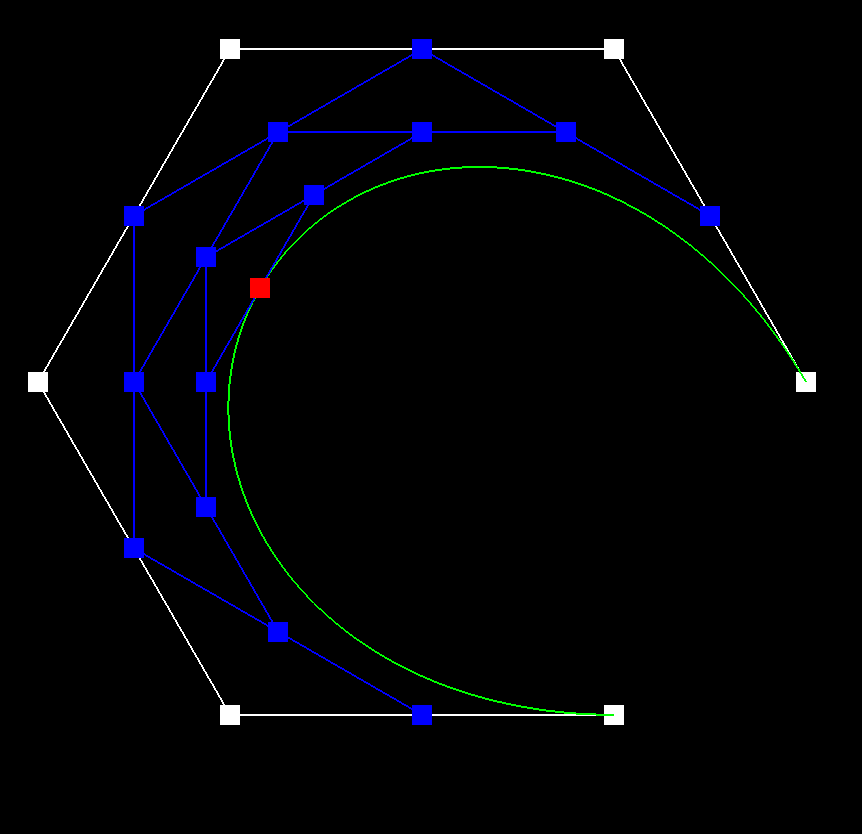
Bézier curves are fundamental in computer graphics, animation, and geometric modeling. The de Casteljau algorithm provides a recursive method to evaluate and subdivide Bézier curves, making it useful for applications like rendering and interpolation.
1D de Casteljau Subdivision Algorithm
The de Casteljau algorithm constructs a Bézier curve by recursively interpolating between control points. Given a set of control points \(( P_0, P_1, \dots, P_n )\) and a parameter \(( t \in [0,1] )\), the algorithm proceeds as follows:
- Compute new interpolated points: \([ P_0^{(1)} = (1 - t) P_0 + t P_1, \quad P_1^{(1)} = (1 - t) P_1 + t P_2, \quad \dots, \quad P_{n-1}^{(1)} = (1 - t) P_{n-1} + t P_n ]\)
- Repeat this process for successive levels: \([ P_0^{(2)} = (1 - t) P_0^{(1)} + t P_1^{(1)}, \quad P_1^{(2)} = (1 - t) P_1^{(1)} + t P_2^{(1)}, \quad \dots, \quad P_{n-2}^{(2)} = (1 - t) P_{n-2}^{(1)} + t P_{n-1}^{(1)} ]\) Continue until a single point remains, which is the curve point at \(( t)\).
Implementation
In my implementation, I itererated through a vector of control points, using the de Casteljau algorithm to compute the next level of points. I was able to make some efficient optimizations by reserving the necessary space for the new points and using emplace_back instead of push_back.
Time (original) w/ length 3: 0.542 µs
Time (original) w/ length 2: 0.25 µs
Time (optimized) w/ length 3: 0.334 µs
Time (optimized) w/ length 2: 0.208 µs
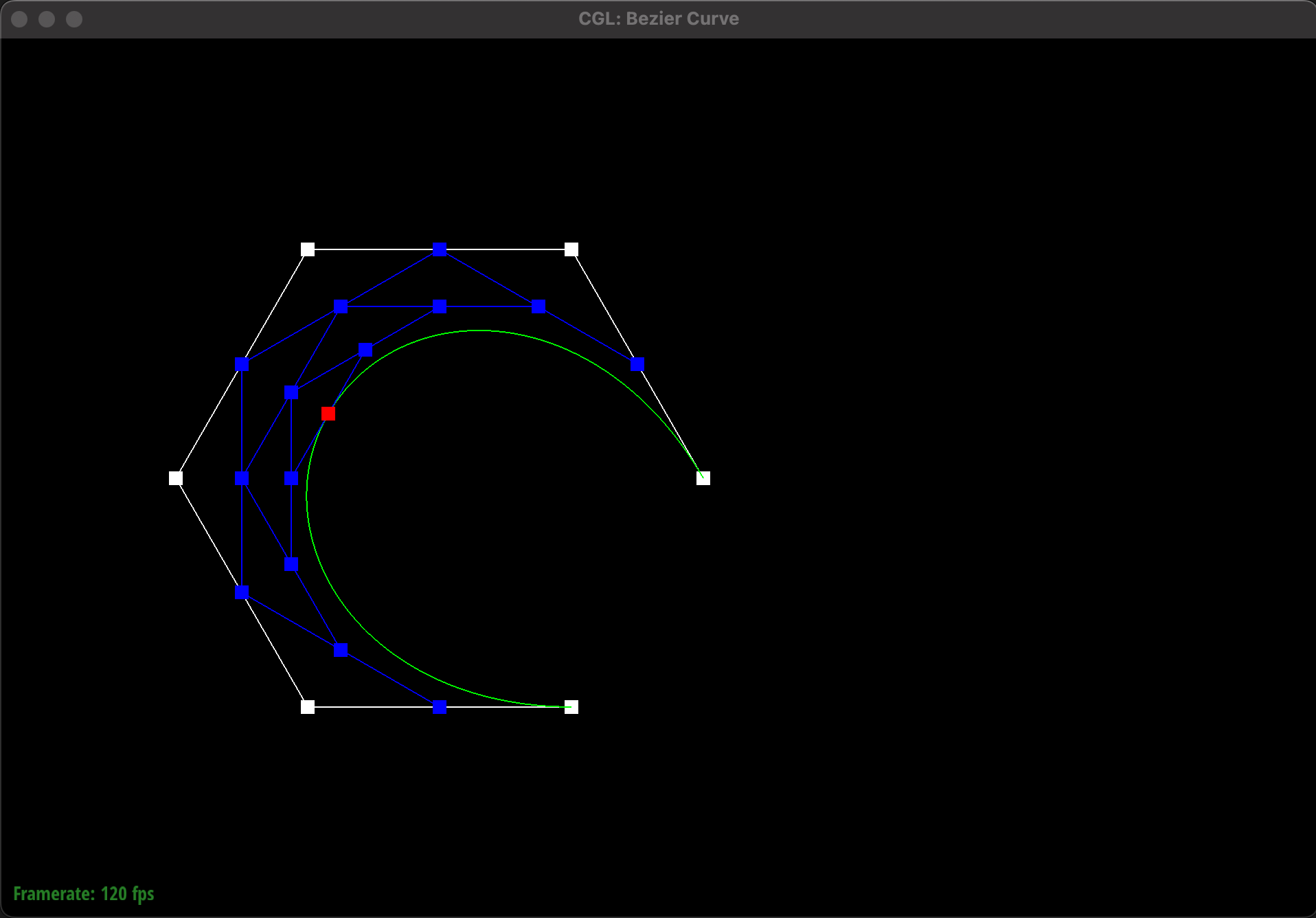
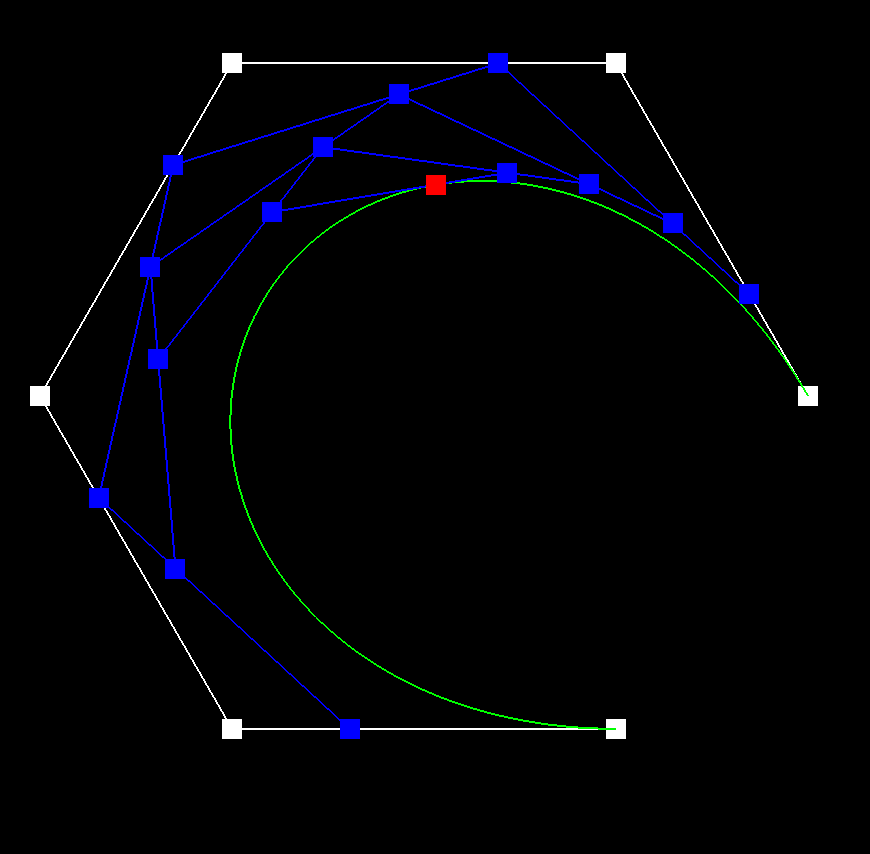
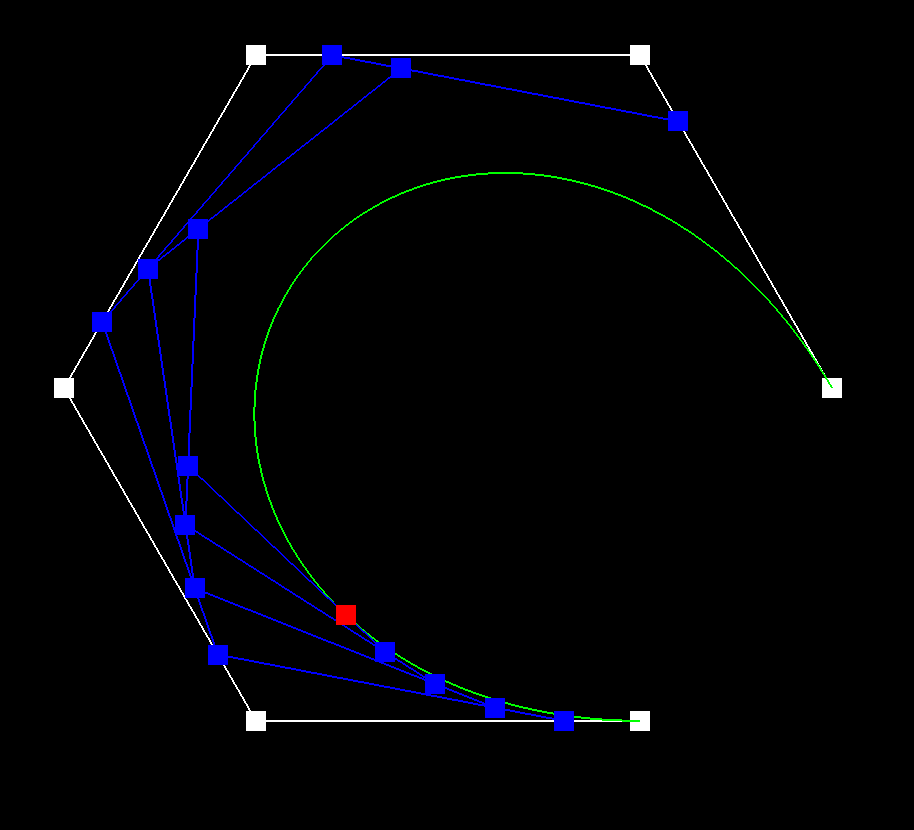
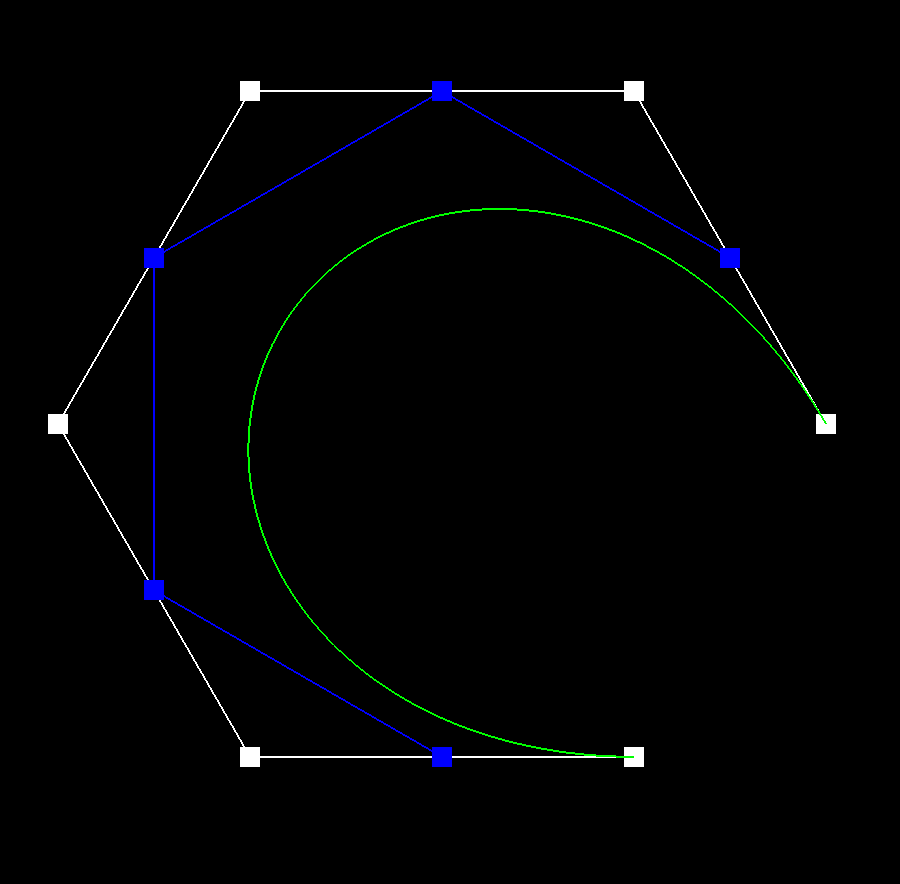
Bézier Surfaces with Separable 1D de Casteljau
Bézier surfaces are a natural extension of Bézier curves, allowing for the representation of complex shapes in 3D space. The de Casteljau algorithm extends naturally to Bézier surfaces by applying the 1D algorithm twice—once along one parameter direction and then along the other. This method leverages the fact that a Bezier surface can be seen as a set of Bezier curves defined in one direction, which can then interpolated in the perpendicular direction.
Extending de Casteljau’s Algorithm to Bezier Surfaces
- Row-wise Reduction (First Pass):
- Each row of control points is treated as a Bezier curve in the
uparameter. - Using de Casteljau’s algorithm for 1D curves, we compute an intermediate set of points—one per row—evaluated at
u.
- Each row of control points is treated as a Bezier curve in the
- Column-wise Reduction (Second Pass):
- The intermediate points from the first pass now define a new Bezier curve along the
vparameter. - Applying de Casteljau’s algorithm again, we compute the final interpolated point on the Bezier surface.
- The intermediate points from the first pass now define a new Bezier curve along the
Implementation
In my implementation, I followed the steps outlined above, iterating through the rows and columns of control points to compute the final surface point. I used a similar optimization strategy as with the 1D de Casteljau algorithm.
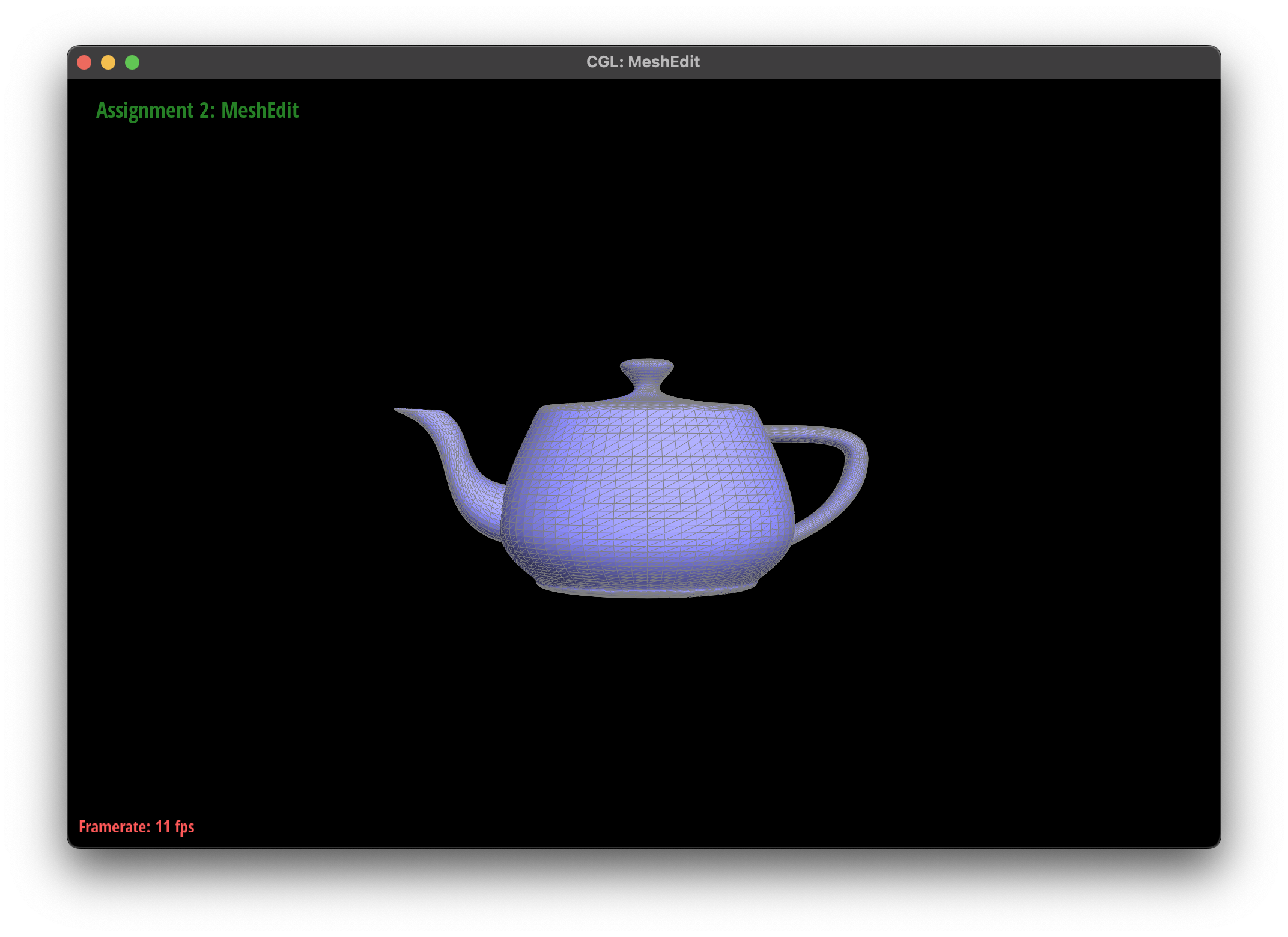
Area-Weighted Vertex Normals
We will now be switching to triangle meshes, as though Bézier surfaces are powerful, they are not as efficient as triangle meshes for rendering. One important aspect of rendering is shading, so we will begin by implementing Phong shading using area-weighted vertex normals.
Algorithm
- Compute Weighted Face Normals:
- For each face incident on a vertex, compute the face normal.
- Weight each face normal by the respective face area.
- Compute Vertex Normals:
- For each vertex, sum the incident weighted face normals.
- Normalize the resulting vector to obtain the vertex’s normal.
Implementation
In my implementation, I traversed the incident faces by first going through the vertex’s halfedge, then calling twin(). With a halfedge pointing back towards our original vertex, I can traverse to the next halfedge and call twin() again. This allows me to travel through all the faces incident on a vertex, accumulating the weighted face normals, until I reach the starting halfedge. I disregard the computation on any faces that are boundaries, and calculate the area by crossing two vectors that make up the triangle and dividing the norm by two. I then weight the face normal by the area and add it to the vertex’s normal, normalizing the accumulated normals at the end of the traversal.
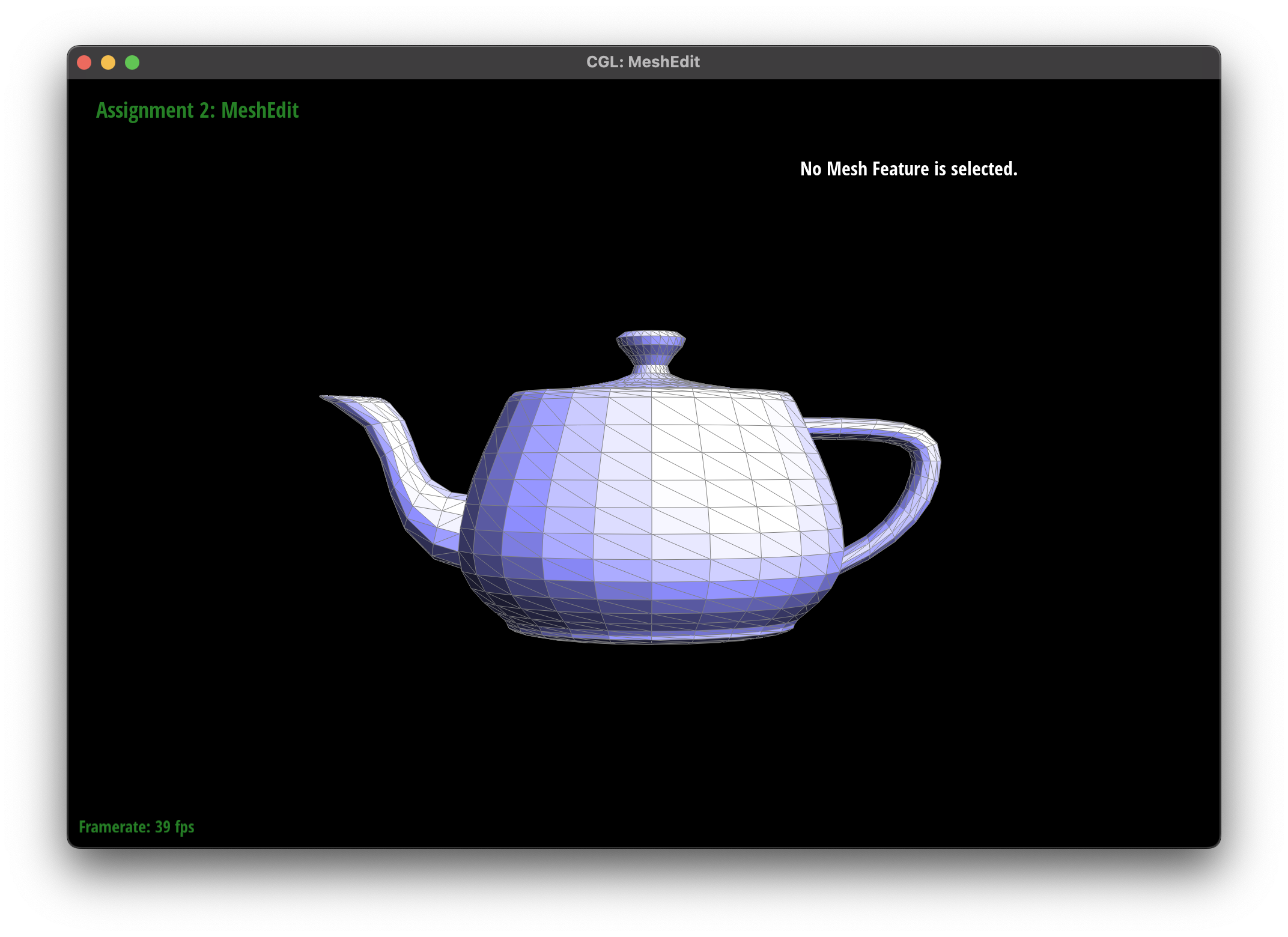
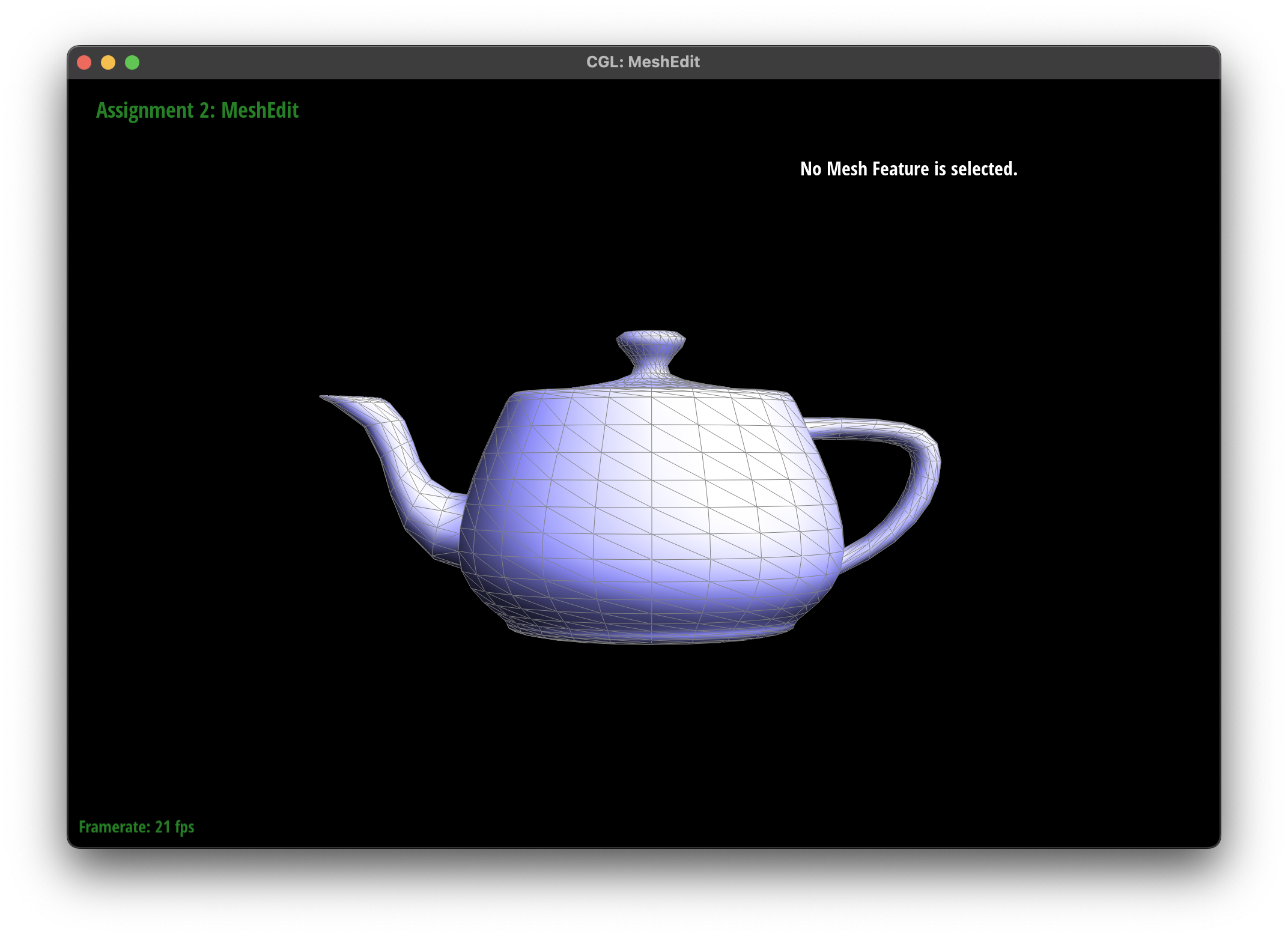
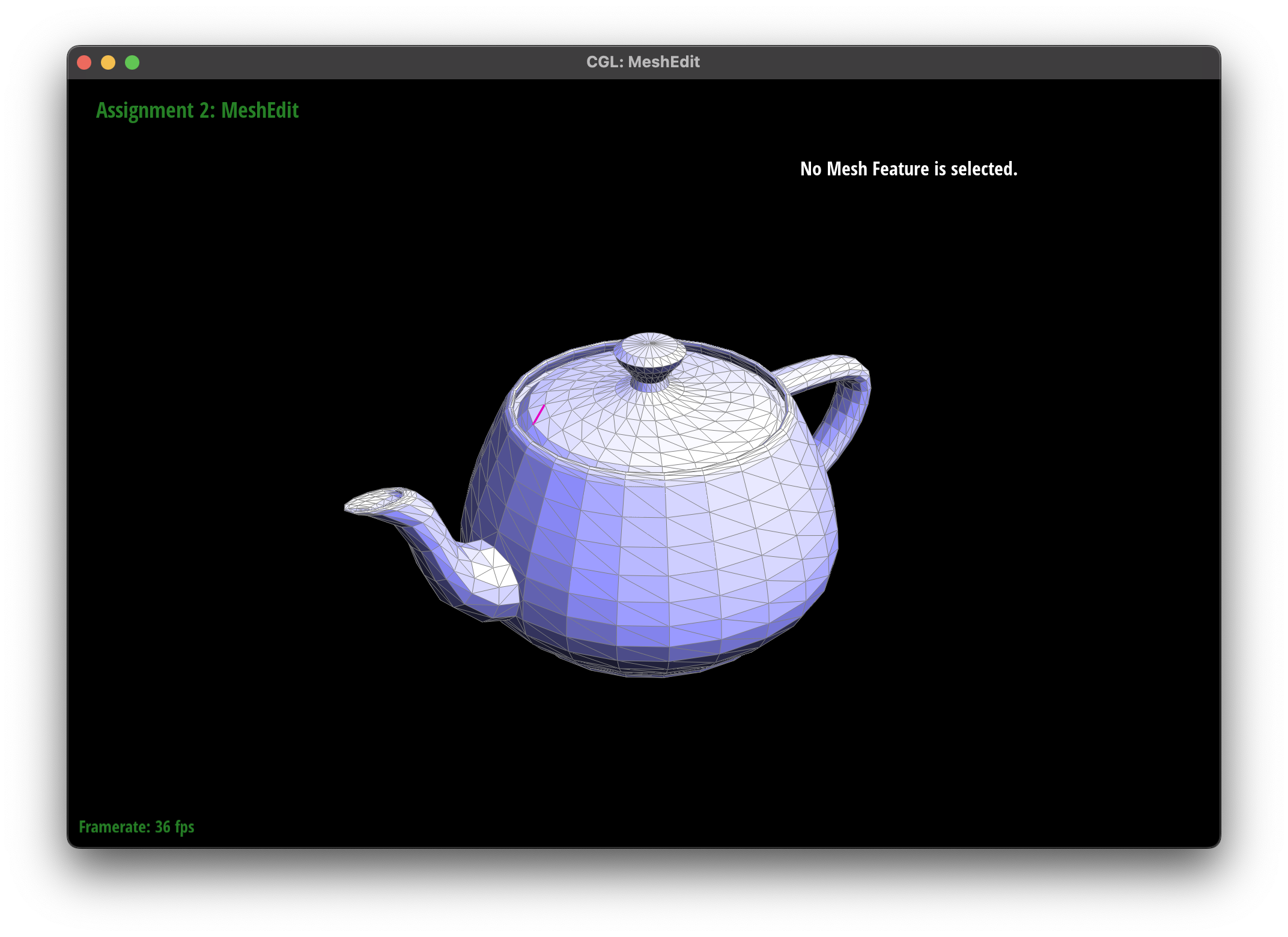
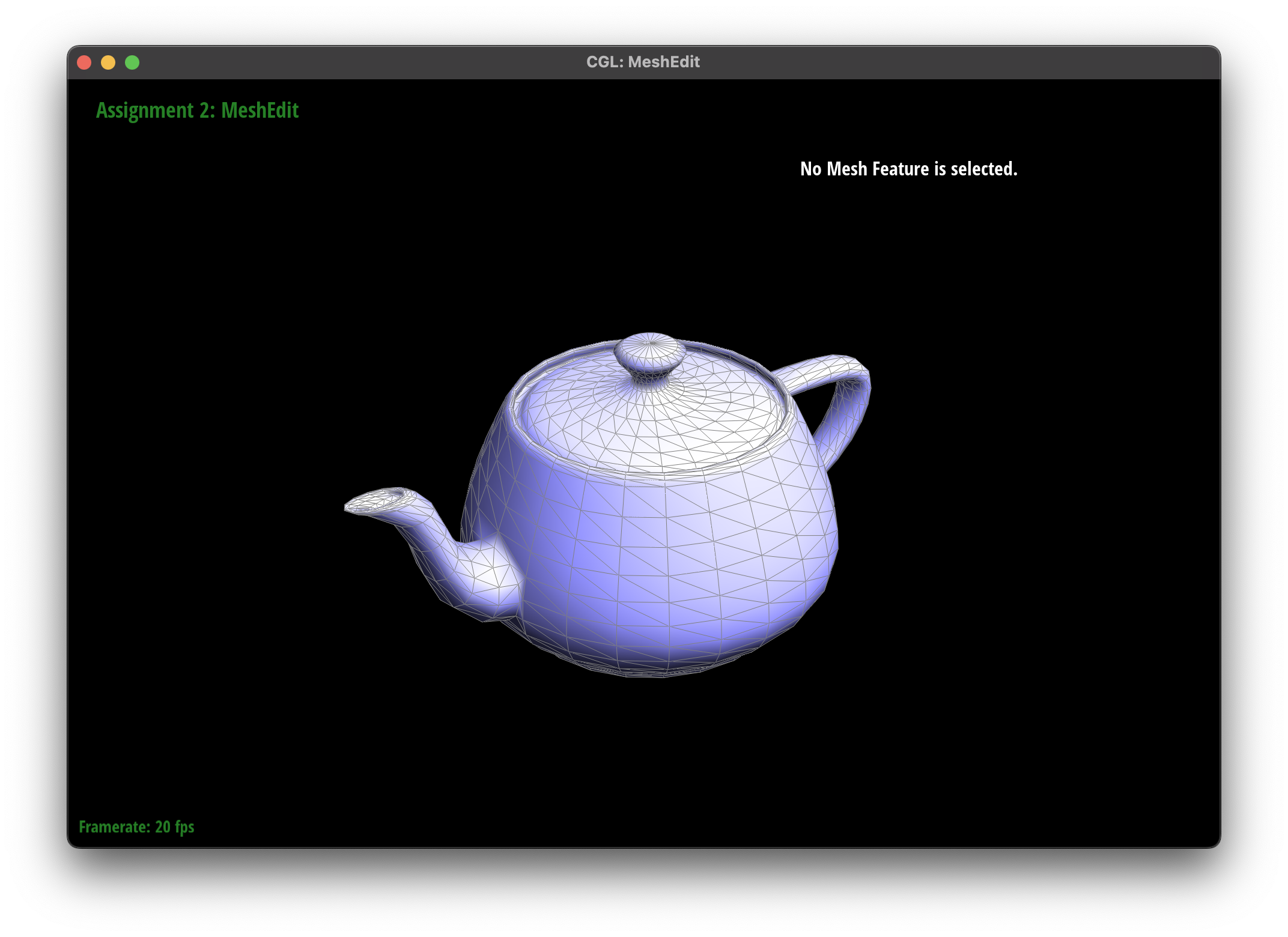
Edge Flip
The edge flip operation is a fundamental operation in mesh processing that swaps the diagonal of a quadrilateral face.
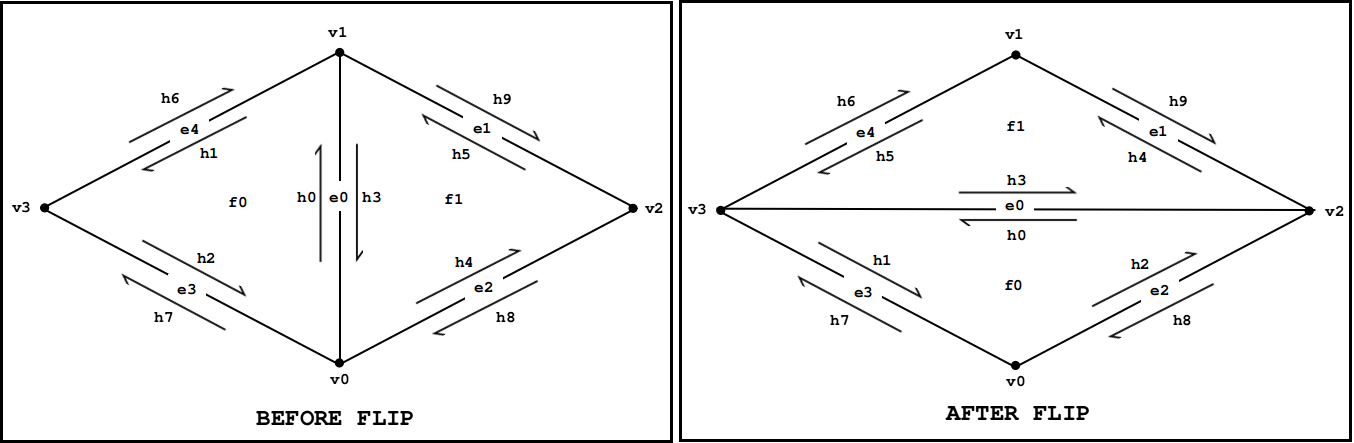
Implementation
In my implementation of edge flipping, I first checked if the edge was a boundary edge, and if so we left it as is. Otherwise, I extracted all relevant halfedges, vertices, and faces, and then reconnected them to form the changed faces.
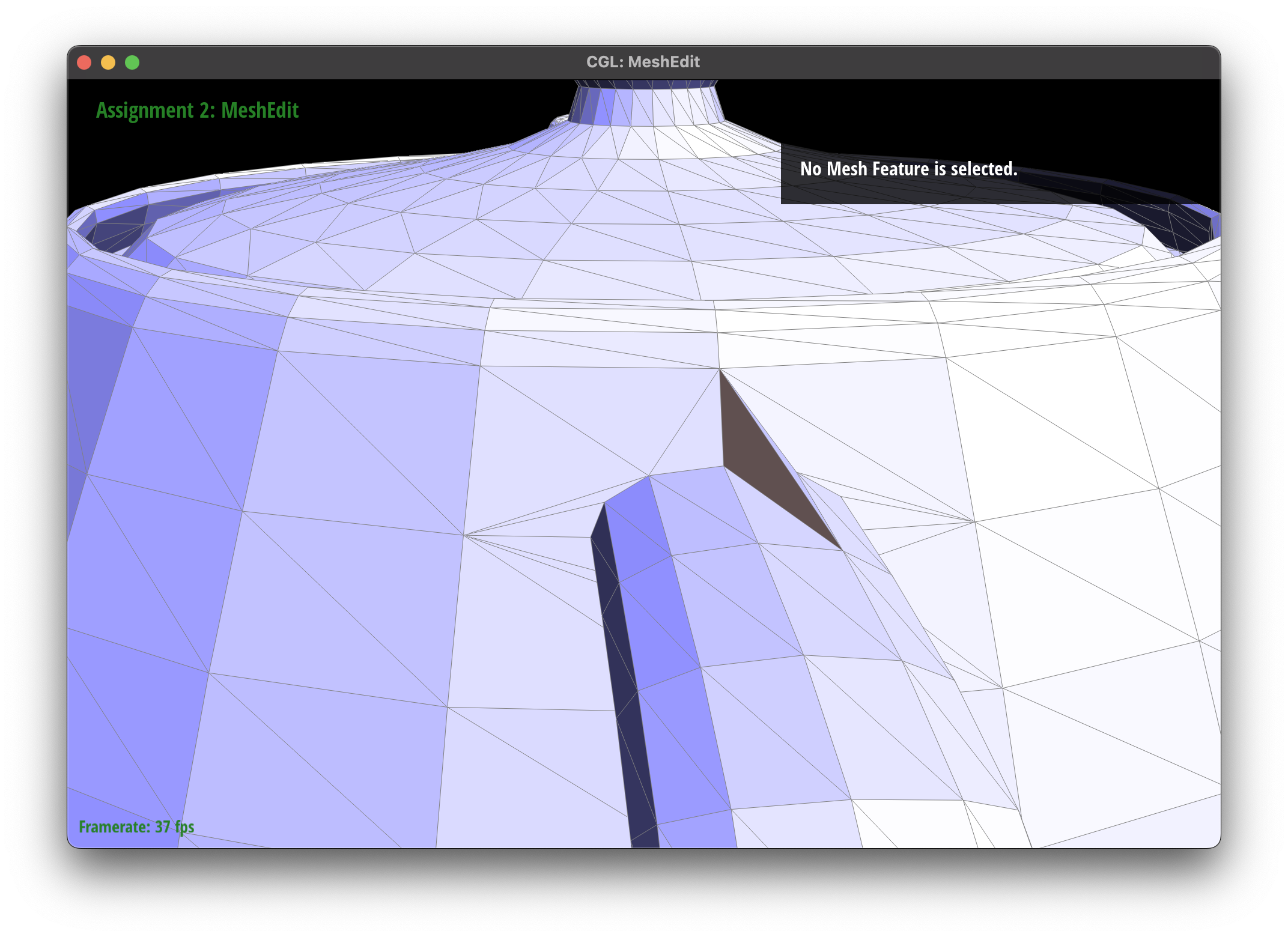
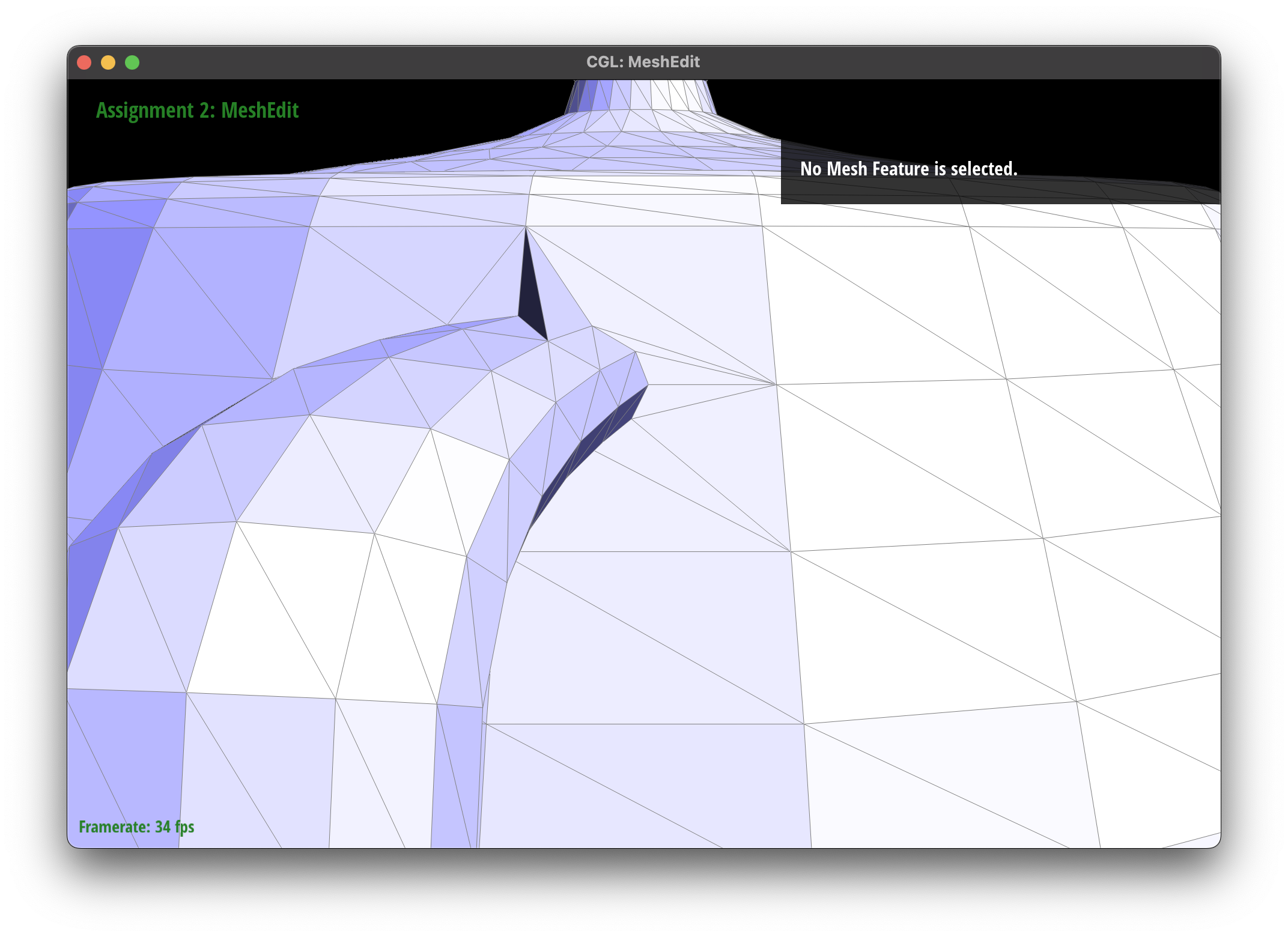
Debugging Journey
I began by drawing an example of the triangle before and after the flip, and then I drew the halfedges and vertices to understand the connections. I then drew the new faces and halfedges to ensure that the connections were correct. Unfortunately, in my first drawing I had mistakenly drawn my halfedges clockwise, leading to an incorrect implementation. Additionally, I spent a large time debugging skinny degenerate triangles that were created by the edge flip operation. I eventually realized that this was expected behavior, as the edge flip operation can create skinny triangles.
Edge Split
The edge split operation is another fundamental operation in mesh processing that splits an edge by adding a new vertex in the middle edge of a quad face which is connected to the side vertices.
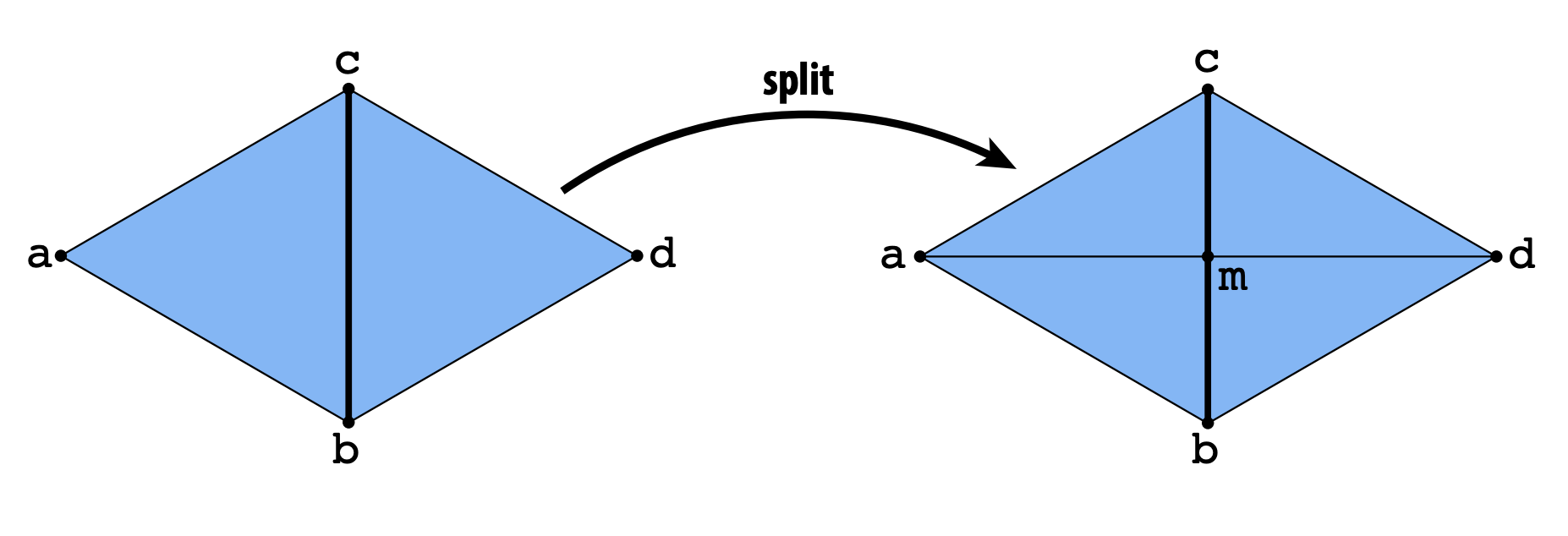
Implementation
My implementation of edge splitting was similar to edge flipping, where I first checked if the edge was a boundary edge. I then extracted all relevant halfedges, vertices, and faces, created 1 new vertex, 2 new faces, 4 new edges, and 6 new halfedges. I reused the existing middle halfedges and two faces, and reconnected all relevant elements to form the new faces.

Debugging Journey
Luckily the extension from flipping to splitting was relatively straightforward, as I was able to reuse the existing halfedges and faces. However, the sheer amount of variables required me to be specific in my naming in order to ensure I was not misplacing any elements. I also had to be careful to ensure that I was connecting the correct vertices and halfedges to the new elements.
Loop Subdivision for Mesh Upsampling
Loop subdivision is a powerful technique for mesh upsampling, creating a smoother and more detailed mesh from an existing one. It works by refining the mesh through a series of steps that involve splitting edges, updating vertex positions, and creating new faces.
Implementation
I implemented it via computing the new vertex positions and positions for new midpoints. Then I split all my original edges and flipped any edges that connected an old vertex to a new one. Finally, I updated all my points with their stored new positions.
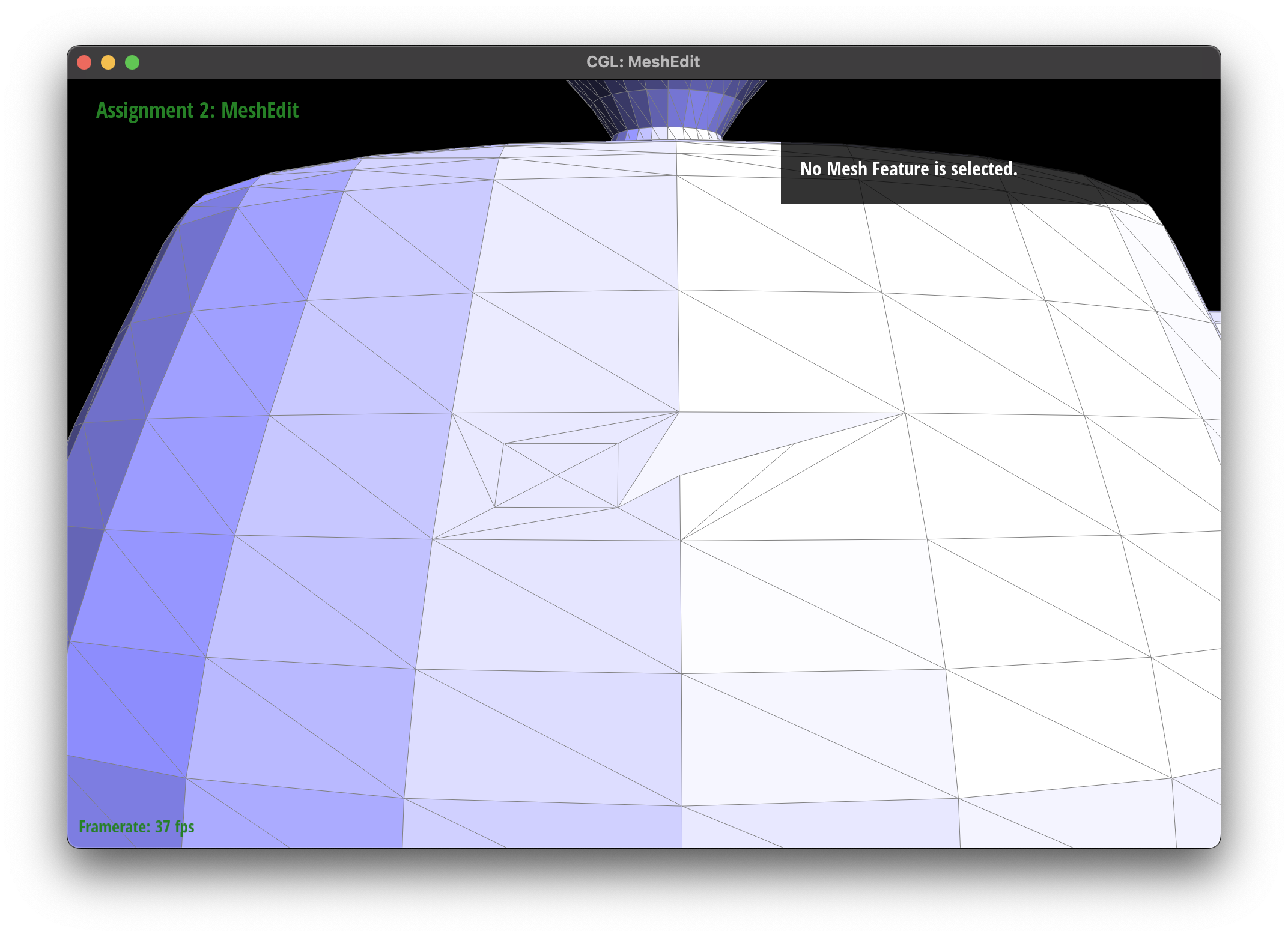
This function caused me to rewrite my edge flip and split functions twice. Turns out the issue was in the upsampling all along, as I was not updating the newly created edges after splitting correctly.
Here are some of the errors I encountered:
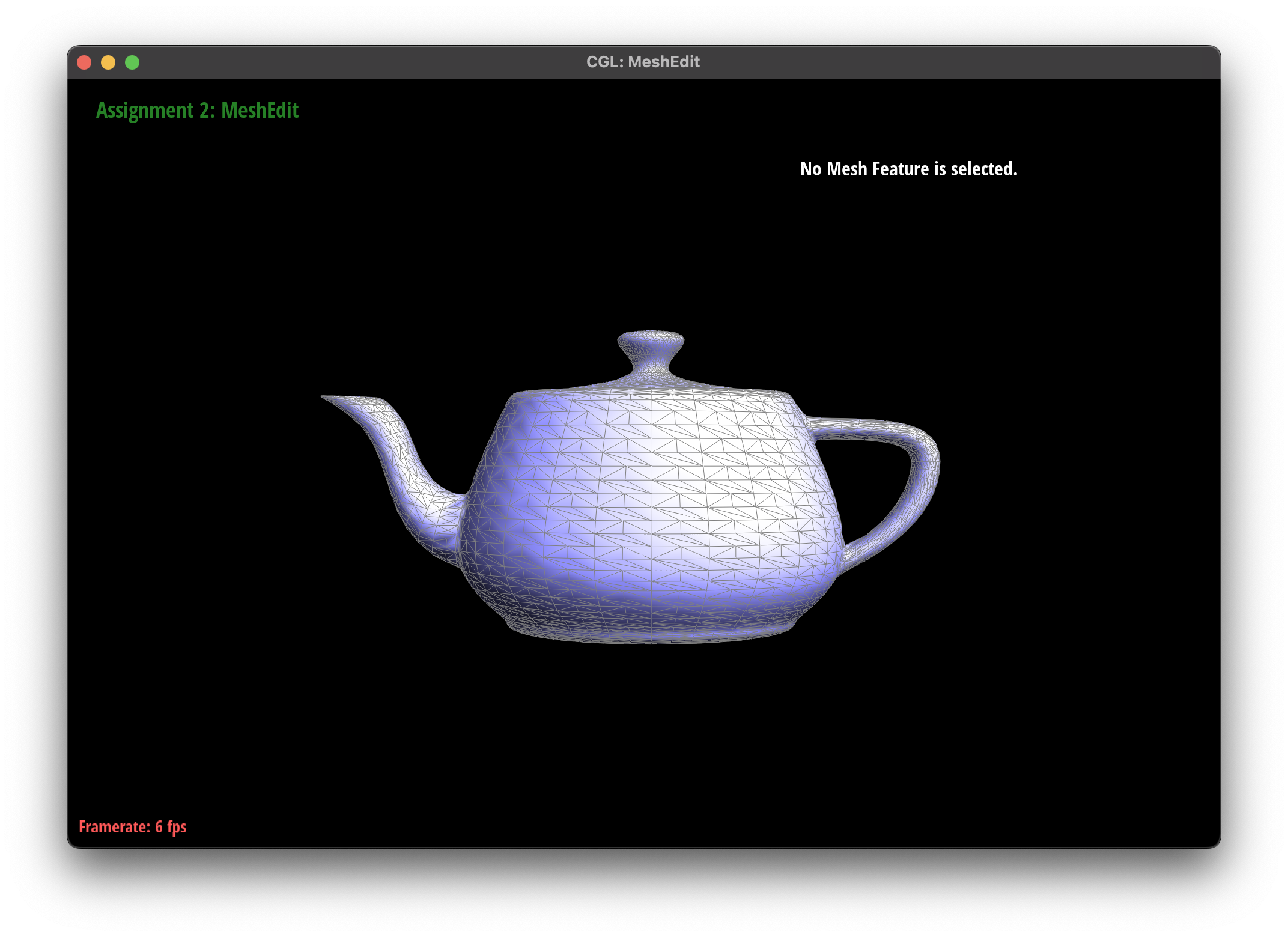
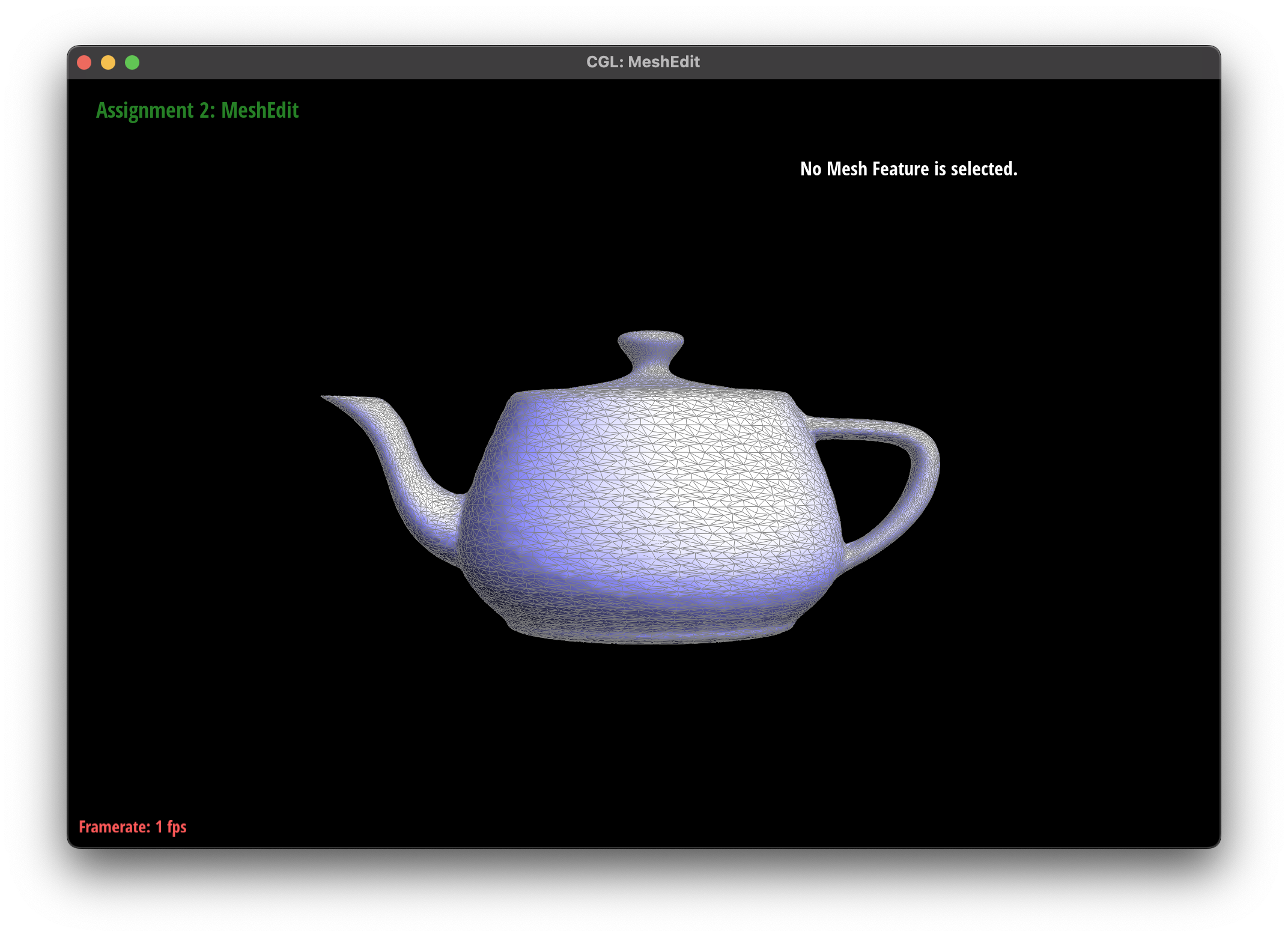
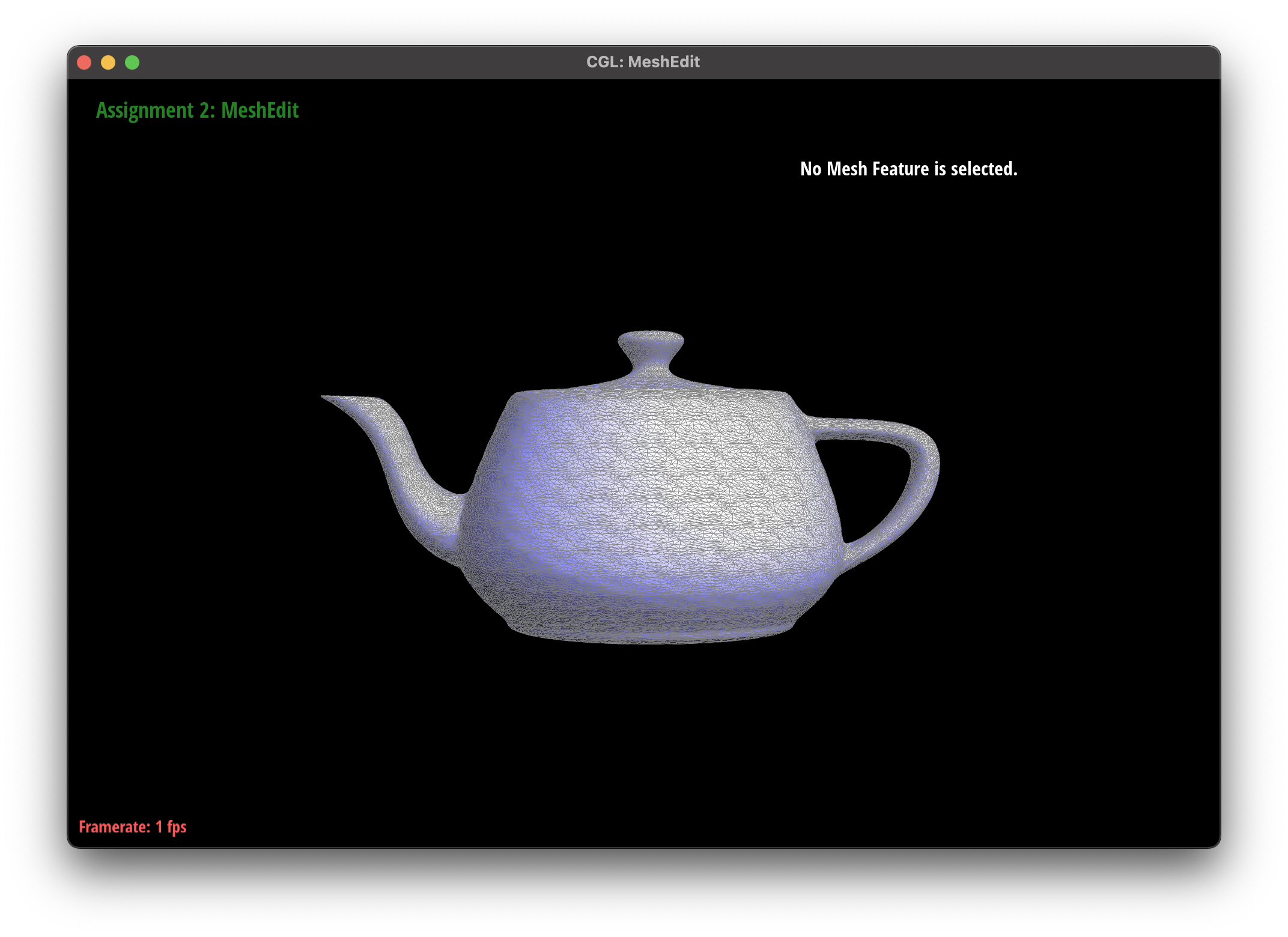
Observations
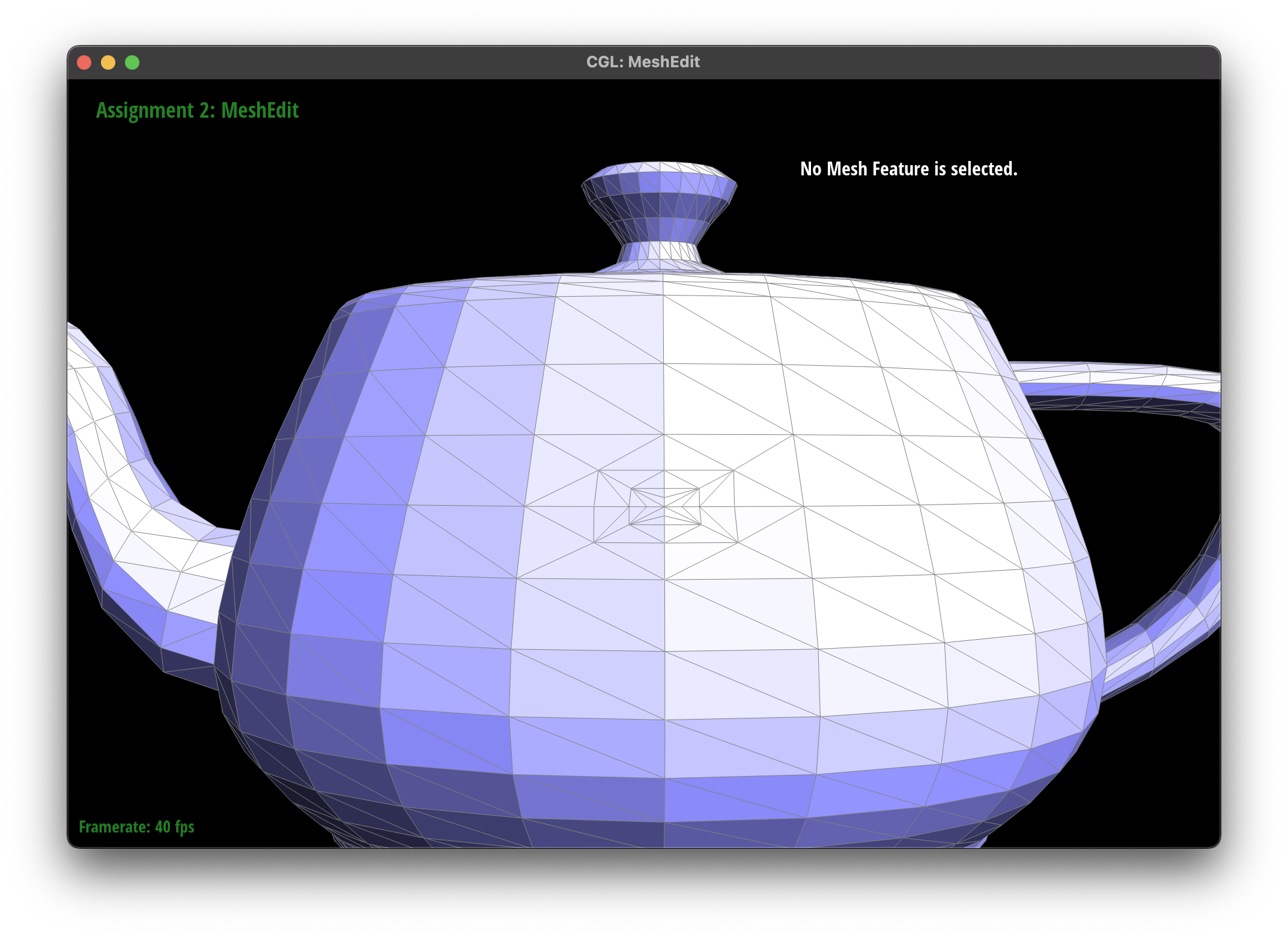
The subdivision algorithm was able to create a smoother mesh for my teapot mesh, as they round out the curves instead of creating sharp edges.
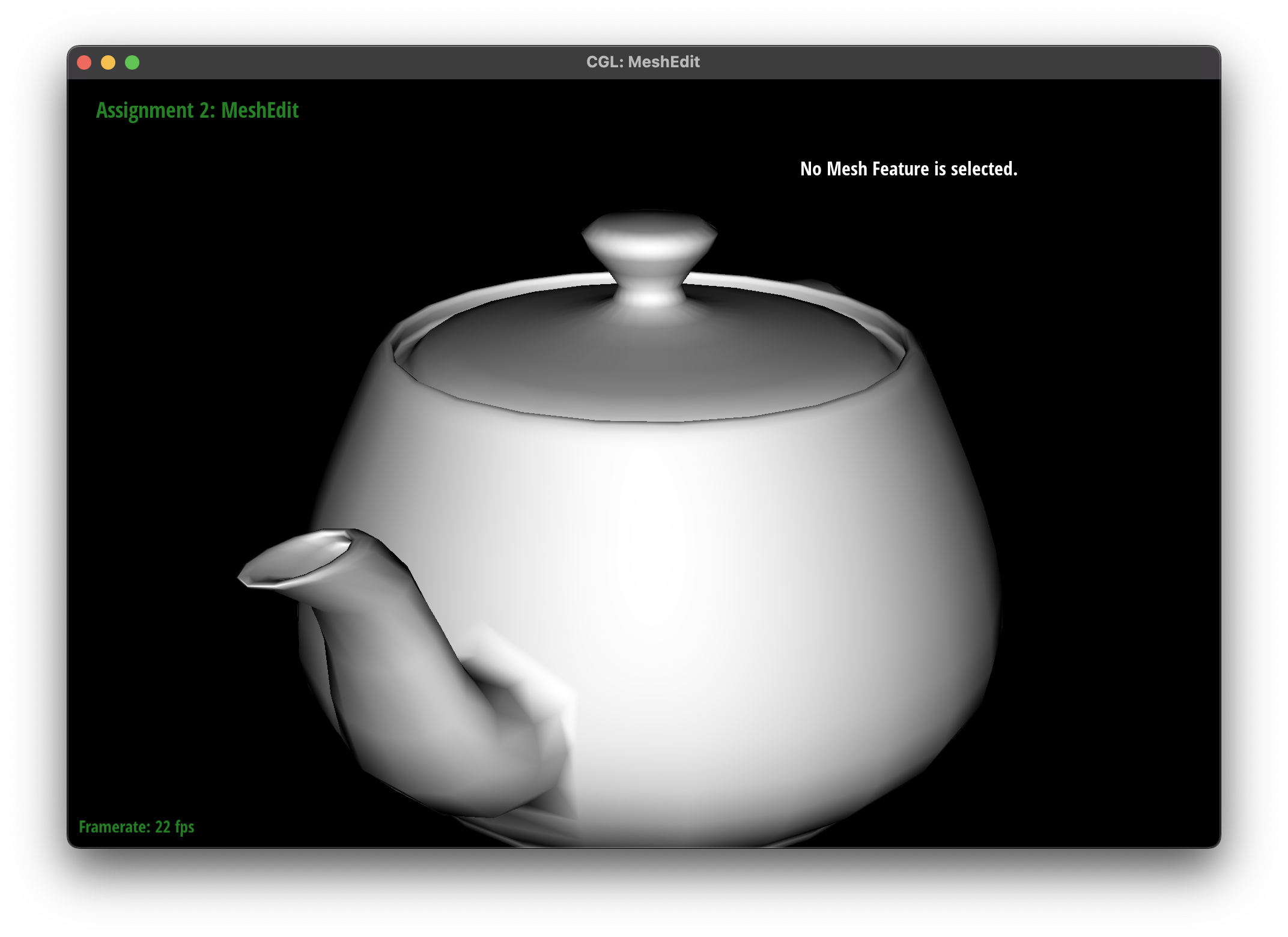
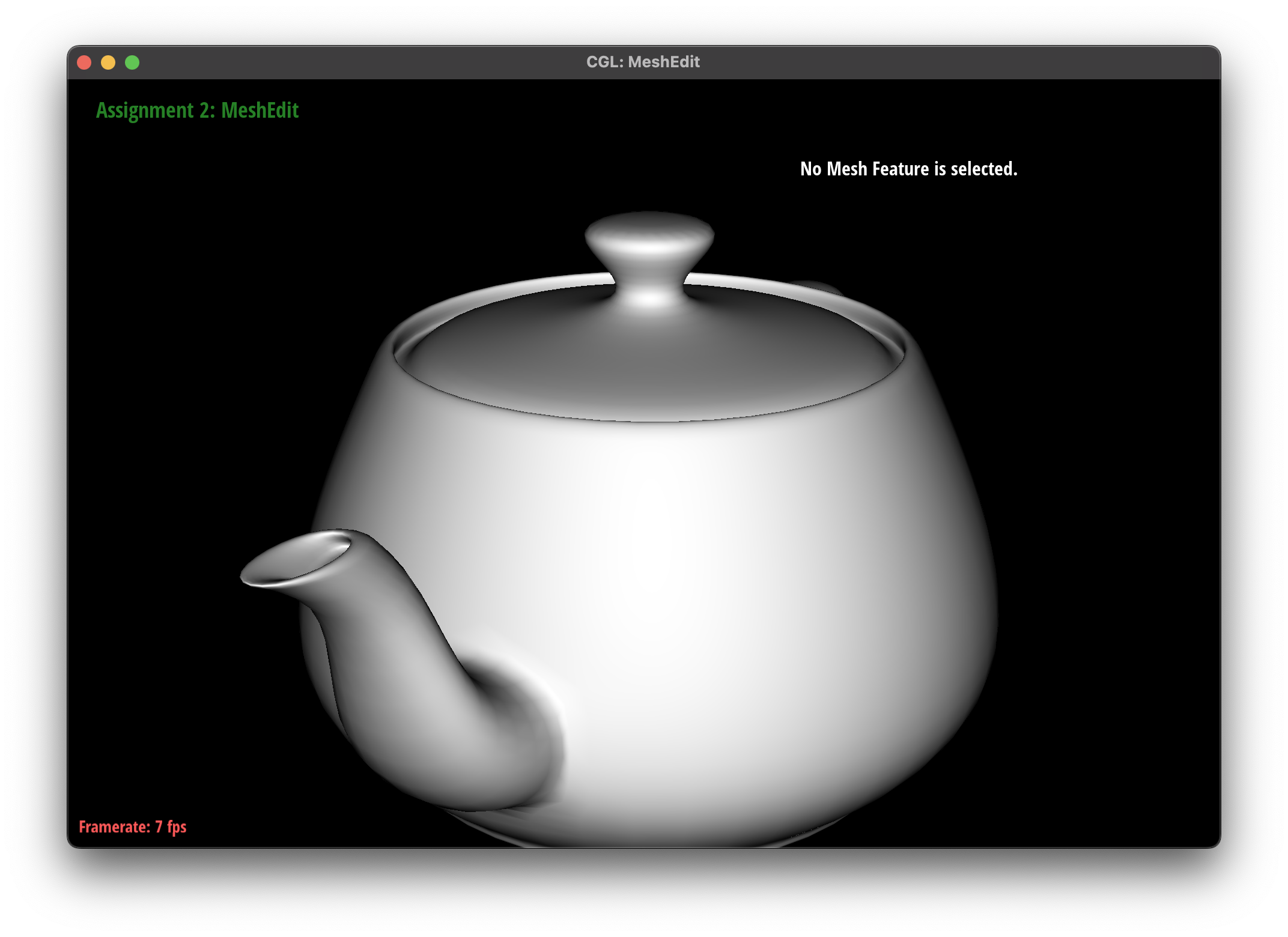
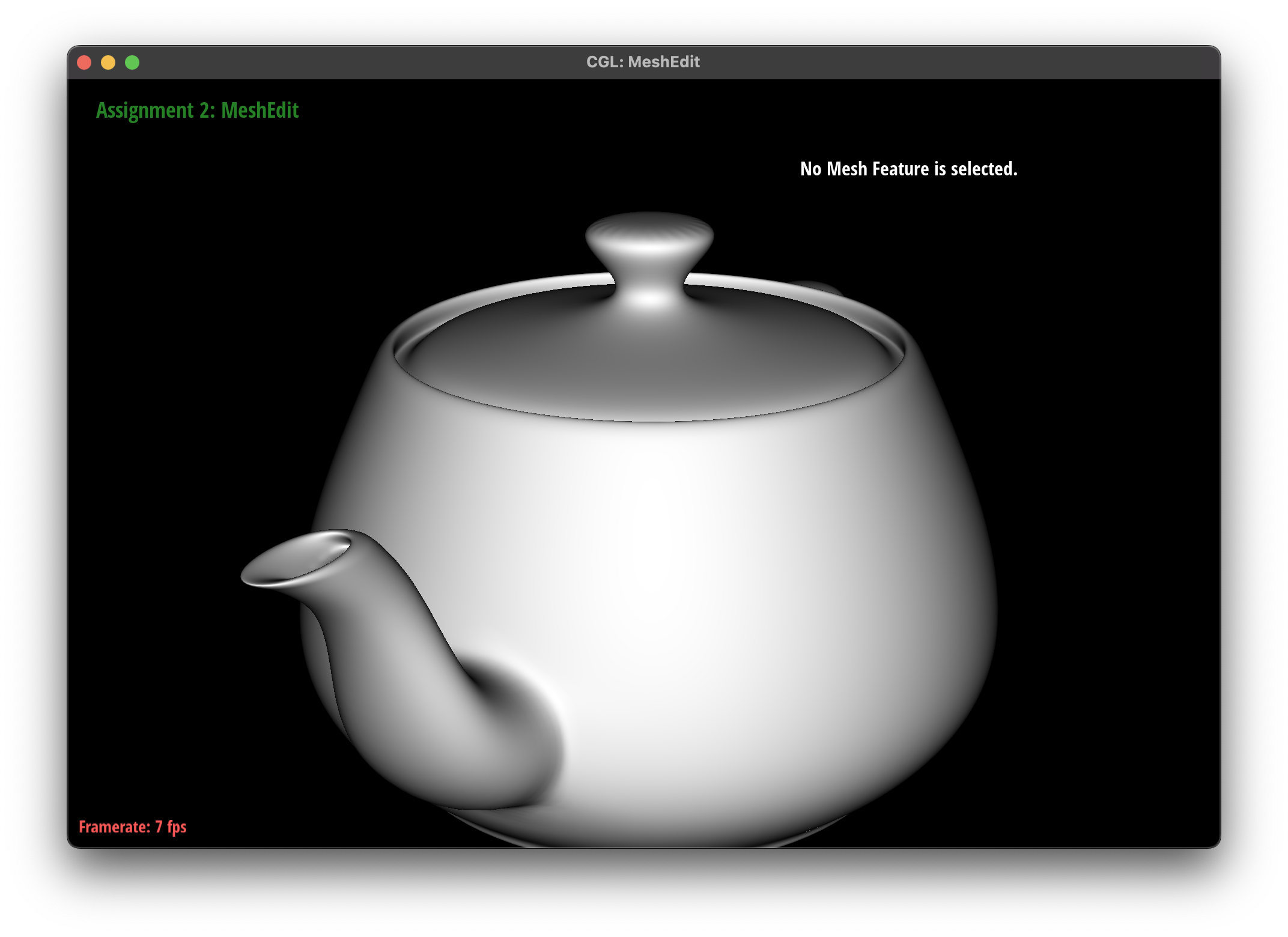
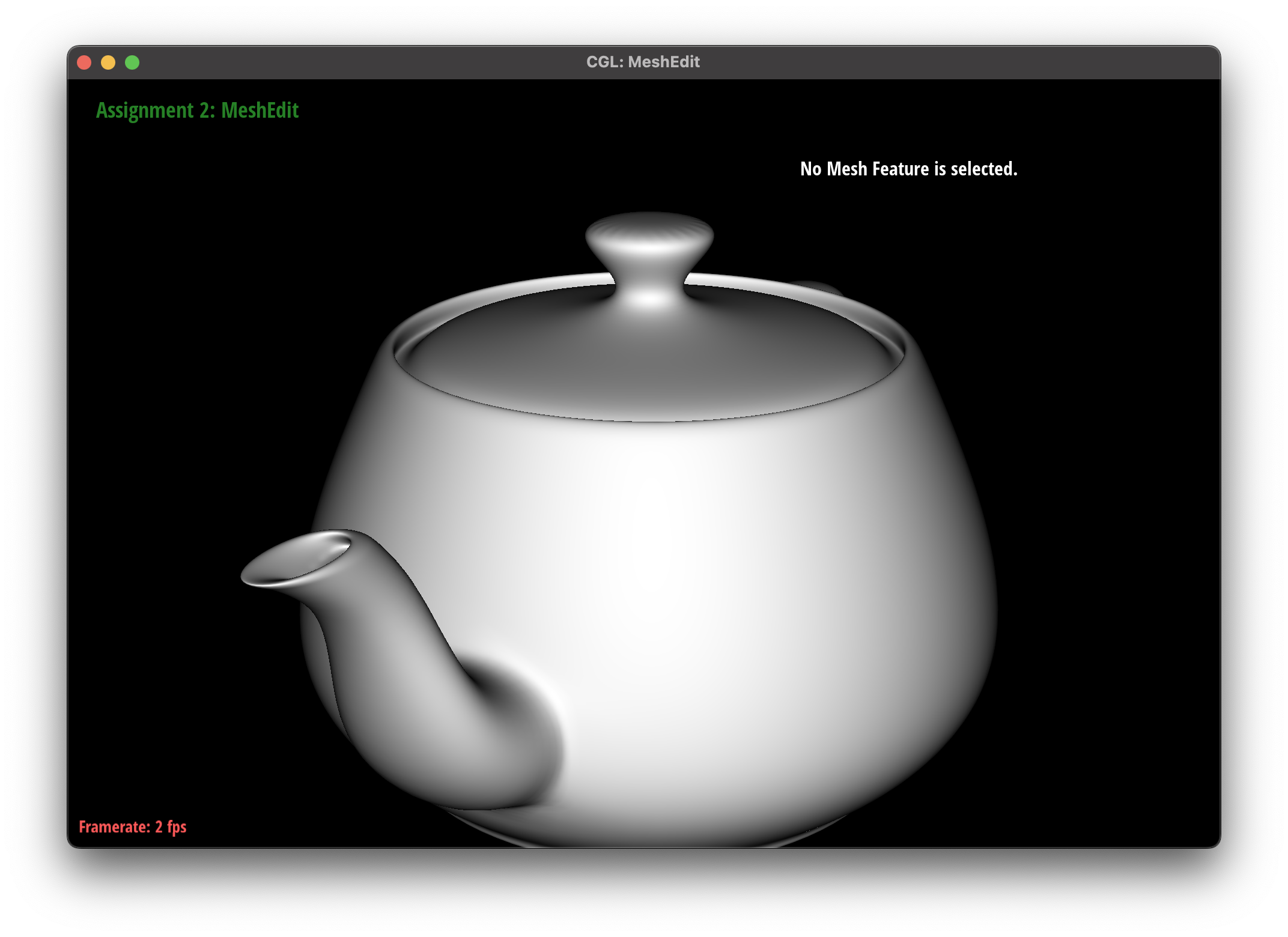
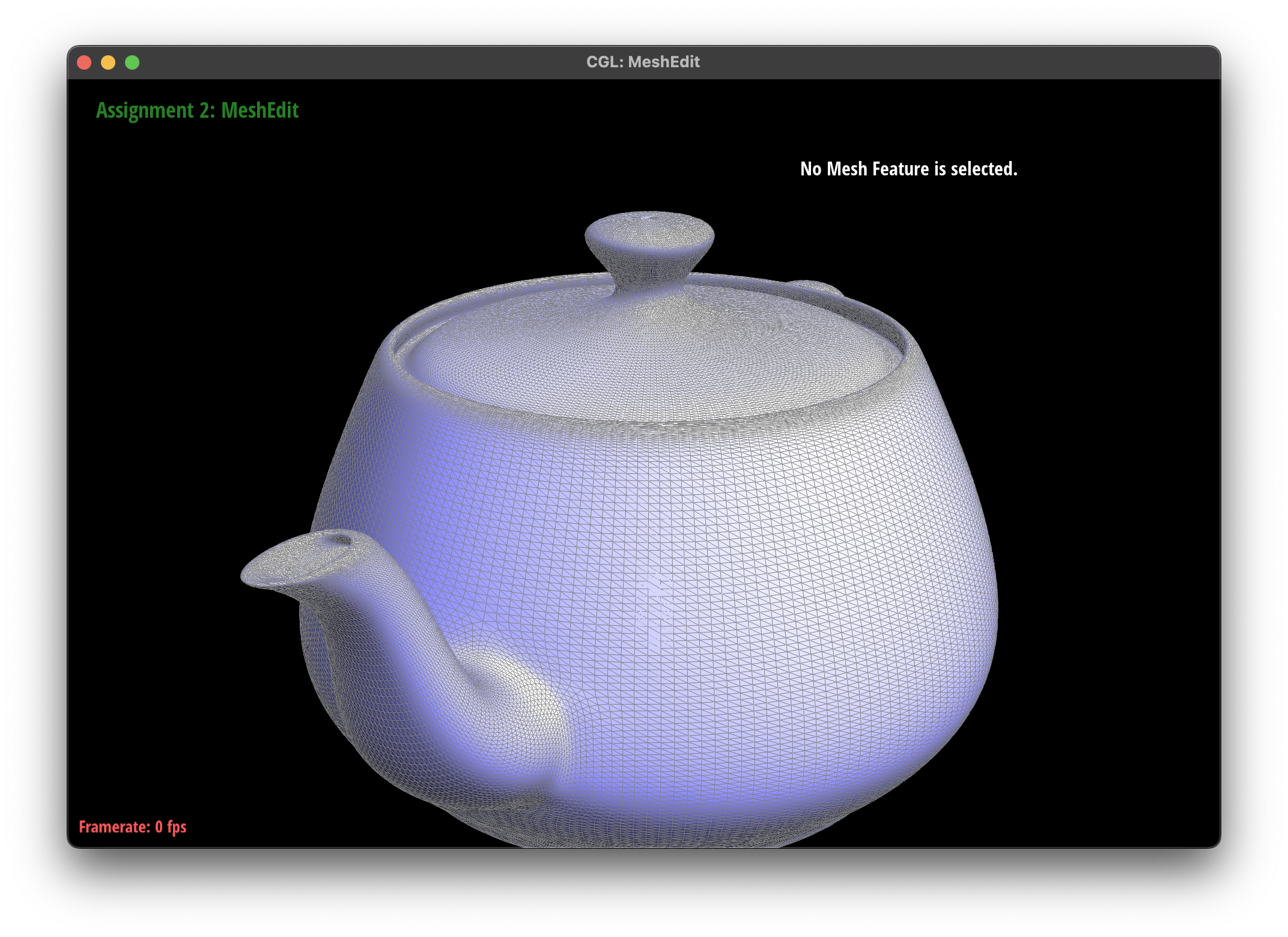
I noticed that presplitting around the handles of the teapot helped to reduce the sharpness of the edges, as the subdivision algorithm was able to round out the edges more effectively. However, there were some areas where the subdivision algorithm had some issues, such as the cube mesh.
In the cube mesh, I noticed that the cube became slightly asymmetric after repeated subdivisions.
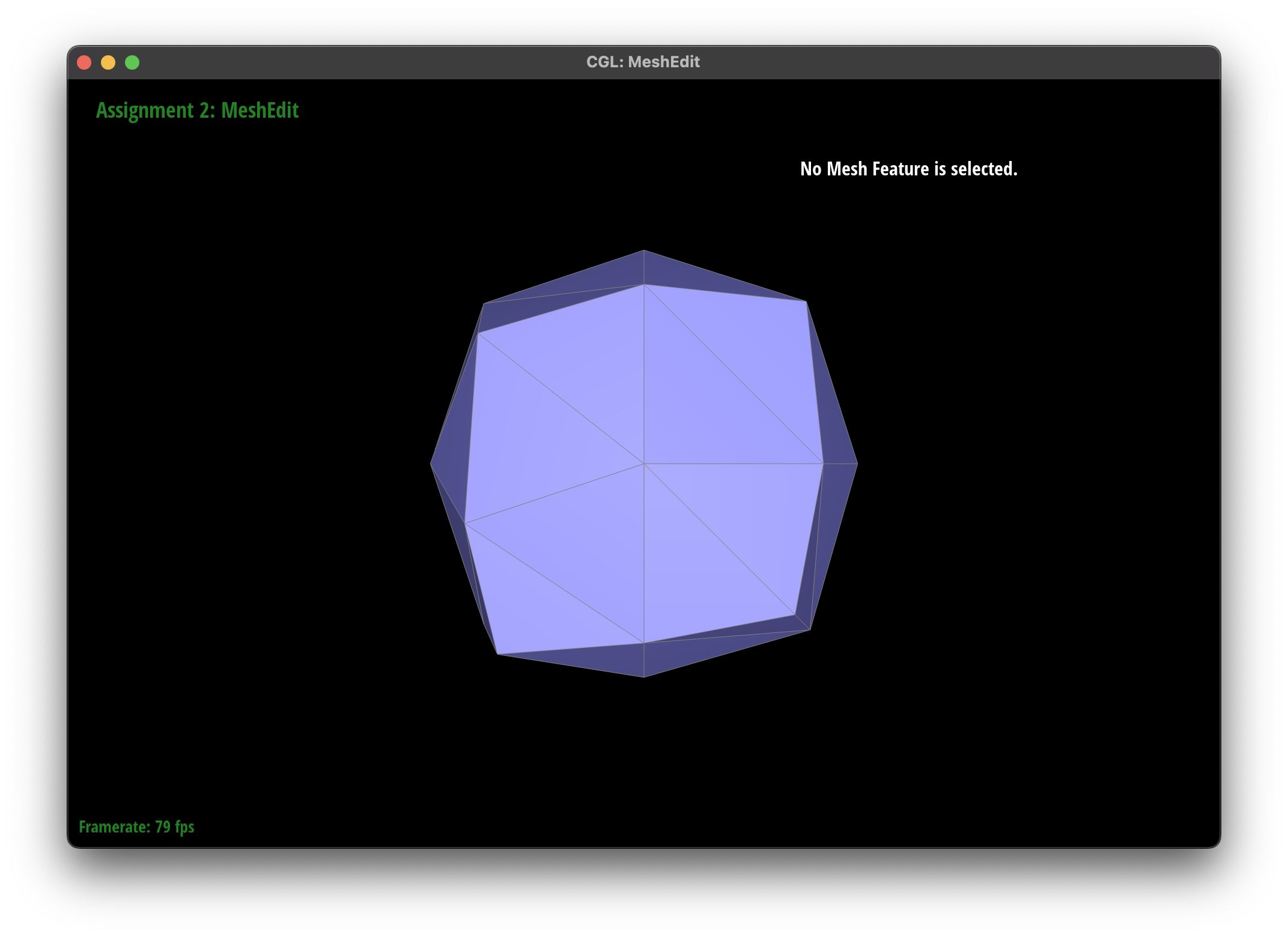
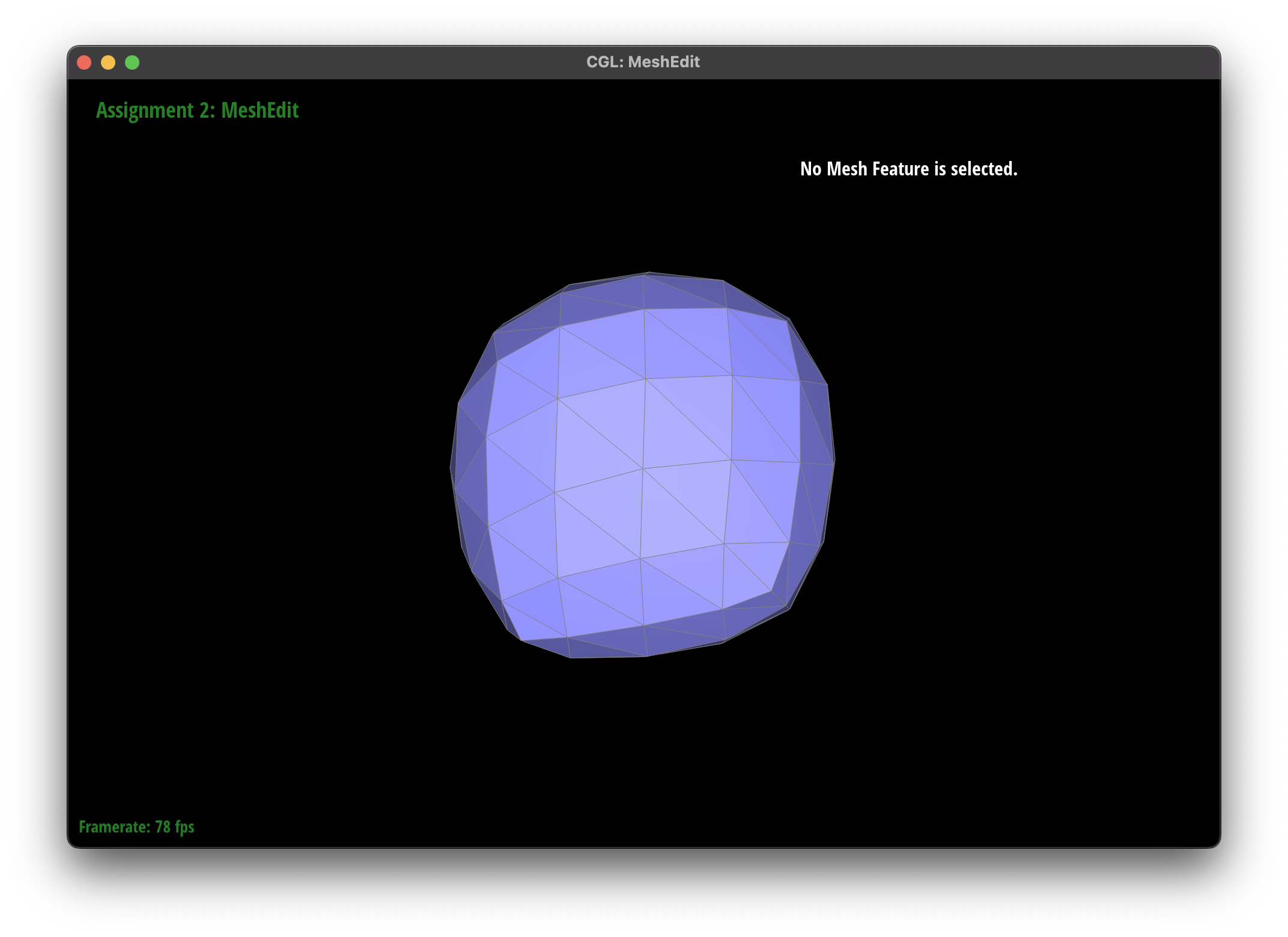
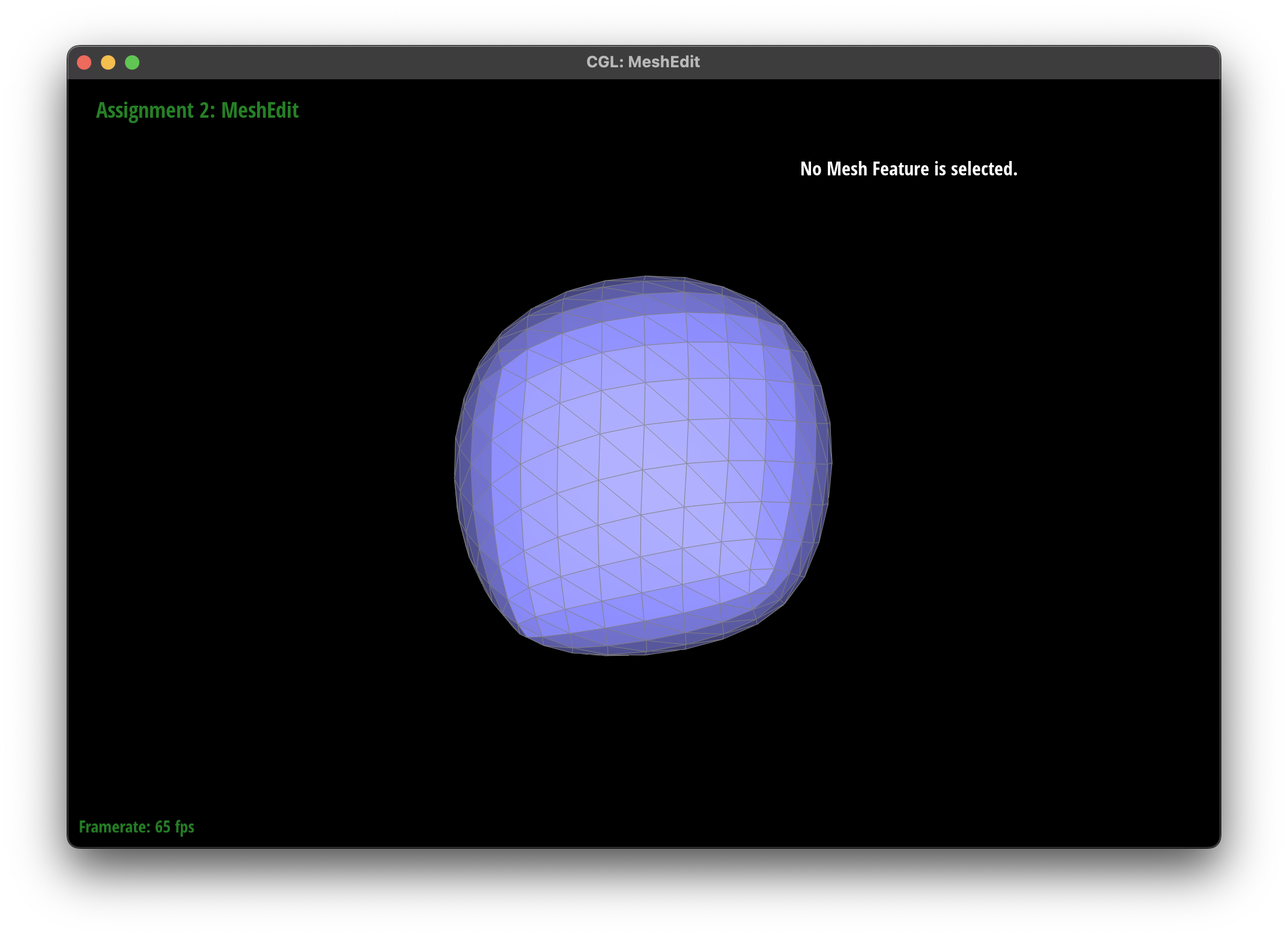
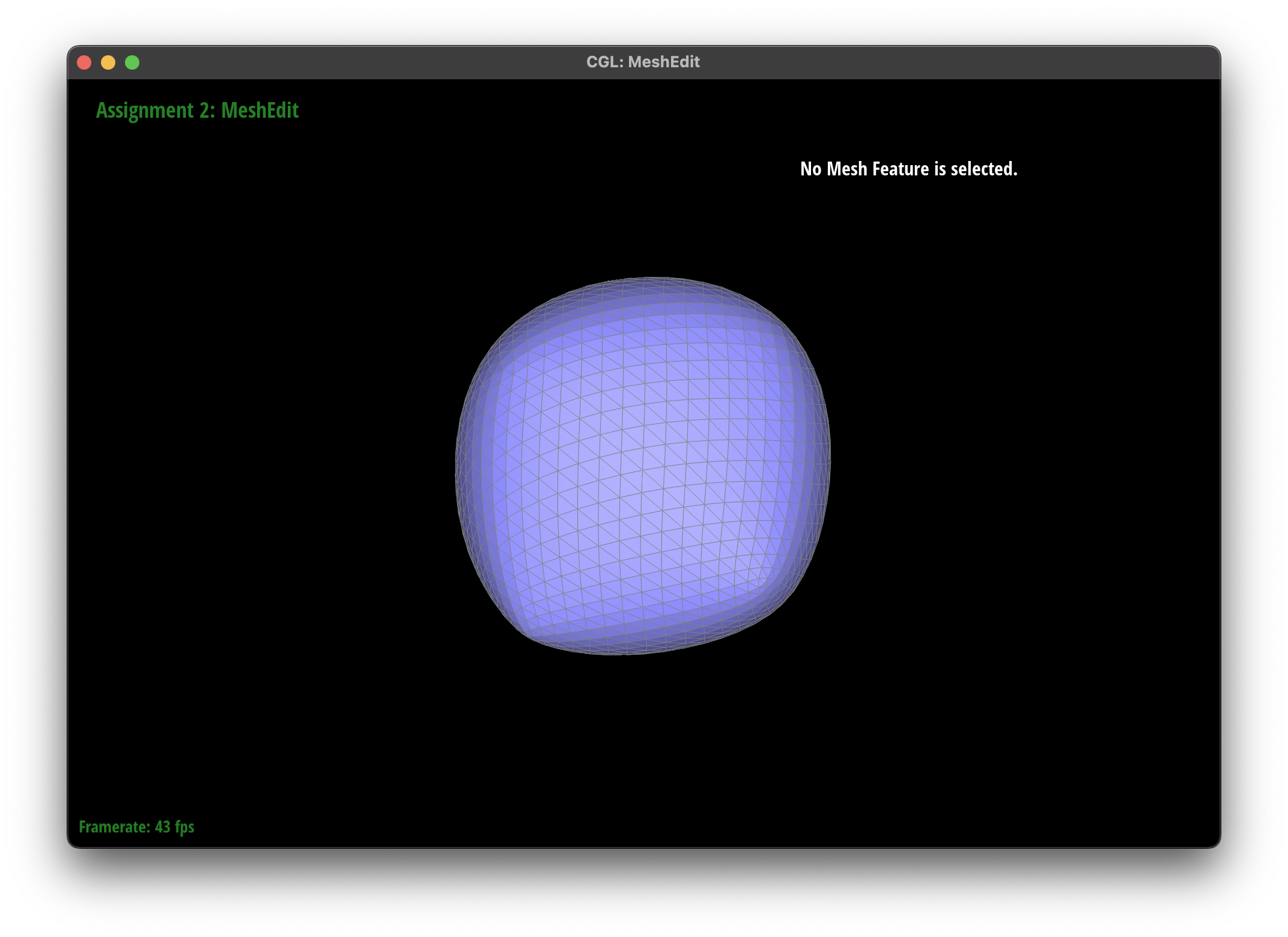
I tried applying some pre splits along a face and noticed that this had some useful effects in reducing the asymmetry.
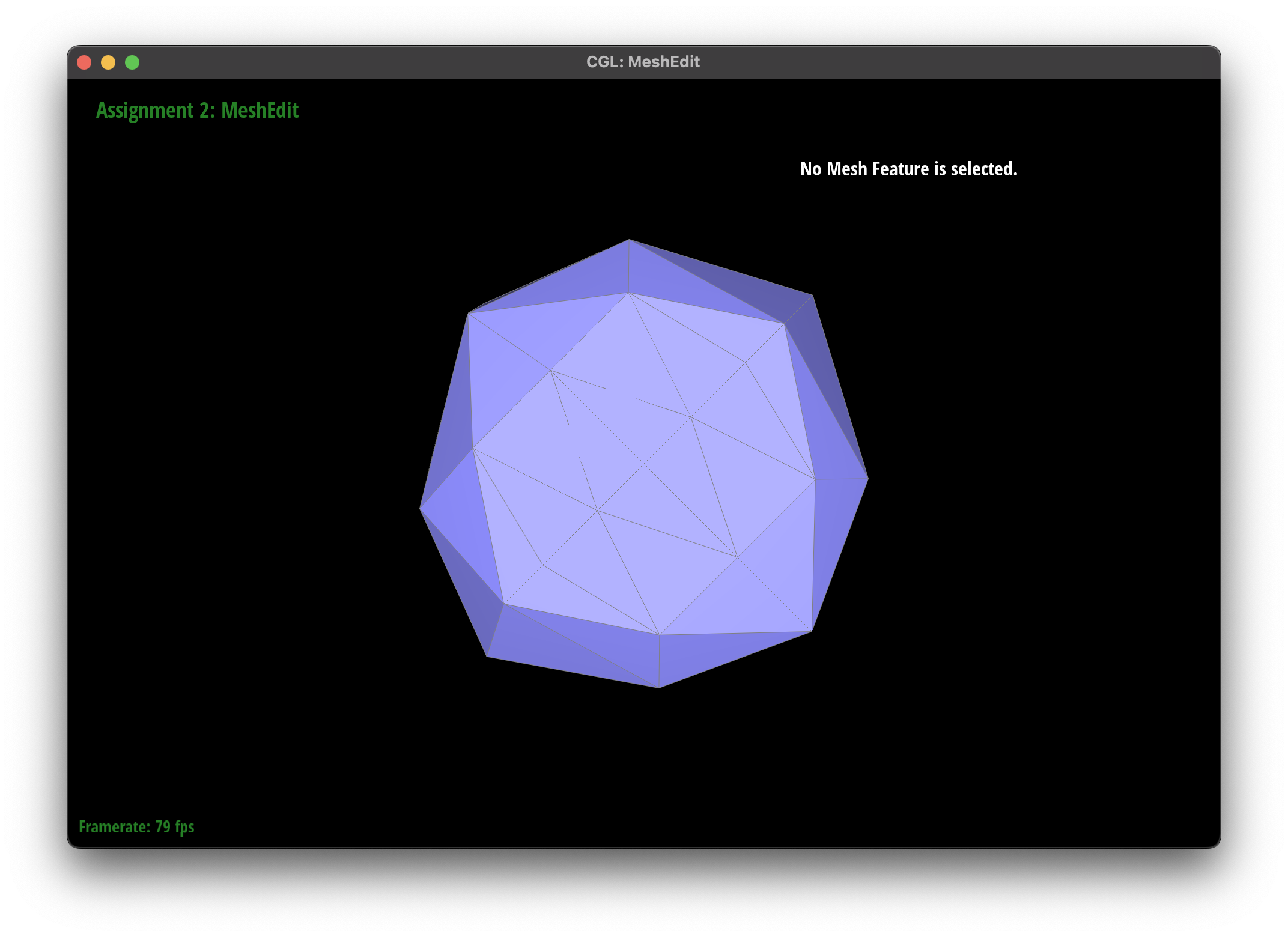
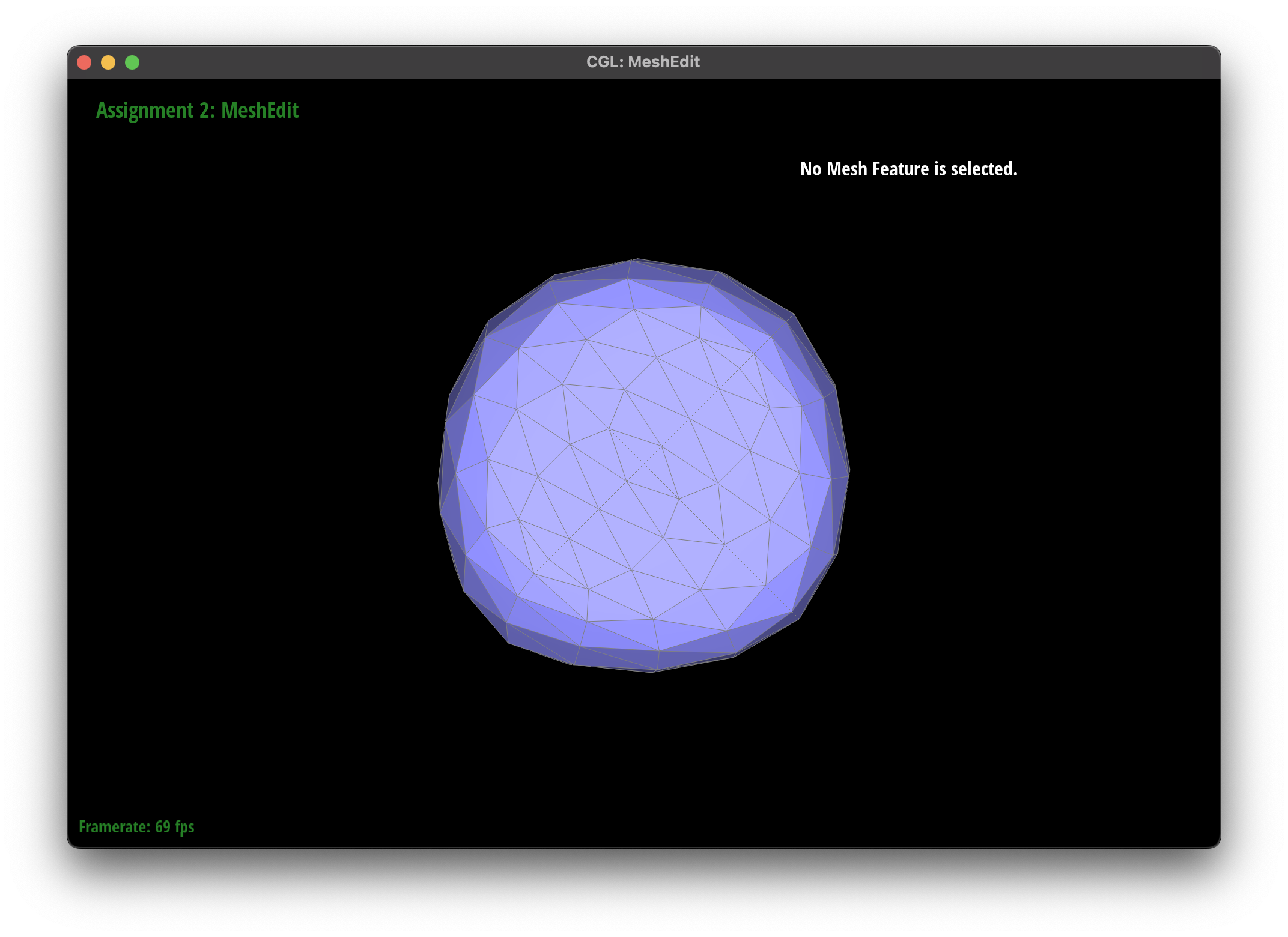
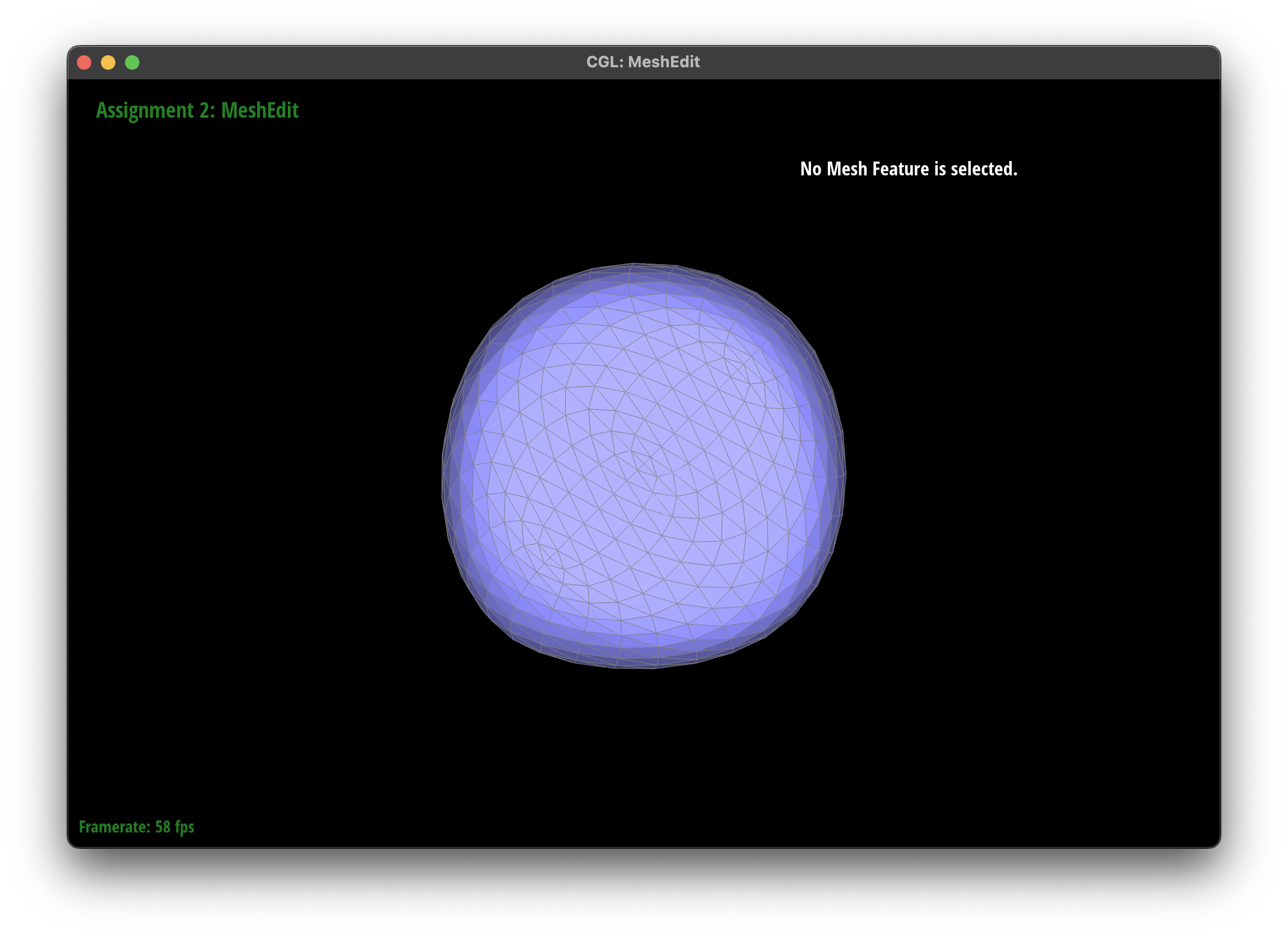
I believe that the pre-splitting helped to alleviate the asymmetry by providing the subdivision algorithm with more information about the mesh, allowing it to create a more symmetric subdivision. This is because although we can represent a cube with a single face, the subdivision may try to smooth out this large face with the edges, leading to the asymmetry.