Path Tracing
Part of CS184 : Foundations of Computer Graphics
Overview
Throughout this assignment, we have implemented a path tracer that simulates the interaction of light with a scene. We began by generating rays for each pixel in the image and tracing them through the scene to determine the point’s normal vector. As the number of primitives increased, the computational cost became prohibitive, so we implemented a Bounding Volume Hierarchy (BVH) to efficiently organize the primitives into a tree structure. This optimization allowed us to quickly discard large portions of the scene that do not intersect with the ray, reducing the number of intersection tests required.
To achieve accurate color computation, we implemented hemispherical sampling using a Monte Carlo estimator to estimate direct lighting at a point. This method simulated the reflection of light on surfaces and determined the light reflected in the camera’s direction. However, a large number of samples were needed for convergence, so we incorporated importance sampling. This method preferentially sampled points of intersection towards light sources, enabling faster convergence by focusing on regions where light contributions were significant.
Despite these improvements, shadowed regions still lacked illumination due to indirect lighting dependencies. To address this, we implemented indirect lighting by recursively tracing rays from intersection points in randomly sampled directions. This simulation of global illumination significantly improved image quality but came with high computational costs. To mitigate these costs, we employed Russian Roulette termination, allowing early termination of some rays based on probability, thus enabling efficient sampling of path lengths. Further, adaptive sampling helped optimize performance by reducing sample counts in regions that converged quickly while increasing them in areas with high variance, ensuring high-quality, low-noise images in reasonable rendering times.
This assignment deepened my understanding of rendering complexities and the trade-offs between computational efficiency and image quality. We explored various sampling techniques and their impact on final render quality. Additionally, we learned the significance of acceleration structures like BVH in optimizing ray intersection tests and improving rendering times for complex scenes.
Ray Generation and Scene Intersection
The first step in path tracing is to generate rays that simulate light transport in the scene. We start by generating a ray for each pixel in the image, and then we trace the ray through the scene to determine the color of the pixel. The ray generation process involves transforming the pixel coordinates into a ray in world space, and the scene intersection process involves finding the intersection of the ray with the scene geometry.
Task 1
We start by modifiying Camera::generate_ray(x, y) to generate a ray in world space corresponding to a given normalized image coordinate (x, y).
Our system is configured as follows: The camera in camera space is positioned at (0,0,0) and looks along the negative Z-axis. A virtual sensor lies on the Z = -1 plane, spanning the field of view (FOV):
-
The bottom-left corner of the sensor is located at:
\[\left(-\tan\left(\frac{hFov}{2}\right), -\tan\left(\frac{vFov}{2}\right), -1\right)\] -
The top-right corner is at:
\[\left(\tan\left(\frac{hFov}{2}\right), \tan\left(\frac{vFov}{2}\right), -1\right)\]
The input (x, y) represents normalized image coordinates where:
-
(0,0)maps to the bottom-left corner of the sensor -
(1,1)maps to the top-right corner
Using linear interpolation, the corresponding sensor space coordinates \((X_s, Y_s, -1)\) are computed as:
\[X_s = (2x - 1) \tan\left(\frac{hFov}{2}\right)\] \[Y_s = (2y - 1) \tan\left(\frac{vFov}{2}\right)\] \[Z_s = -1\]The ray originates at the camera’s position in camera space \((0,0,0)\), and its direction is defined by the vector from the camera position to the sensor point:
\[\mathbf{d}_{camera} = \left( X_s, Y_s, Z_s \right)\]To ensure the ray direction is a unit vector, it must be normalized:
\[\mathbf{d}_{camera} = \frac{\mathbf{d}_{camera}}{\|\mathbf{d}_{camera}\|}\]The camera-to-world transformation matrix \(C_{2W}\) is applied to the ray direction to transform it into world space:
\[\mathbf{d}_{world} = C_{2W} \cdot \mathbf{d}_{camera}\]Again, the direction must be normalized:
\[\mathbf{d}_{world} = \frac{\mathbf{d}_{world}}{\|\mathbf{d}_{world}\|}\]And finally, we set the ray’s origin, which is simply the camera’s origin in world space:
\[\mathbf{o}_{world} = \mathbf{o}_{camera}\]Task 2
We can now construct multiple rays for a given pixel by sampling uniformly within the pixel’s area. This is done by generating a random offset for each ray within the pixel’s area and adding it to the normalized image coordinates. The ray is then generated using the new coordinates, and we can estimate the overall pixel’s recived radiance by averaging the radiance of all rays.
\[\mathbf{offset} = \left( [0,1], [0,1] \right)\] \[\mathbf{r}_i = \text{generate_ray}(x + \mathbf{offset}\_x, y + \mathbf{offset}\_y)\] \[\mathbf{radiance} = \frac{1}{\text{ns_aa}} \sum_{i=1}^{\text{ns_aa}} \text{est}(\mathbf{r}_i)\]Task 3
Next we can begin with implementing the ray intersection with the scene, starting with triangles. We use the Möller-Trumbore algorithm to determine if a ray intersects a triangle. The algorithm is based on the idea of finding the intersection point of the ray with the plane defined by the triangle, and then checking if the intersection point lies within the triangle.
The algorithm is as follows:
\[\vec{e}_1 = \vec{p}_1 - \vec{p}_0 \quad \vec{e}_2 = \vec{p}_2 - \vec{p}_0\] \[\vec{s} = \vec{o} - \vec{p}_0 \quad \vec{s}_1 = \vec{d} \times \vec{e}_2 \quad \vec{s}_2 = \vec{s} \times \vec{e}_1\] \[\begin{bmatrix} t \\ b_1 \\ b_2 \end{bmatrix} = \frac{1}{\vec{S}_1 \cdot \vec{E}_1} \begin{bmatrix} \vec{S}_2 \cdot \vec{E}_2 \\ \vec{S}_1 \cdot \vec{S} \\ \vec{S}_2 \cdot \vec{D} \end{bmatrix}\]For the cost of 1 division, 27 multiplications, and 17 additions, we can determine a time at which the ray intersects the triangle (given that the denominator is not zero), and the barycentric coordinates of the intersection point. We can check if the time falls within the interval \([t_{min}, t_{max}]\) and if the barycentric coordinates are within the range \([0, 1]\), and if so we update our ray’s \(t_{max}\) and save information about the intersection. To compute the normal at our intersection, we can use our barycentric coordinates to interpolate each vertex’s normal at the intersection point.
Task 4
Finally, we can implement the ray intersection with spheres. We start off with our definition of a spherical plane \(p:(p-c)^2 - R^2 = 0\). Since we want to find the intersection of the ray and the surface, we can replace \(p\) with our ray formula \(o +td\). This algorithm is based on the idea that we can know there is an intersection at time \(t\) when the distance between the ray at time \(t\) and the sphere’s center is equal to the sphere’s radius. This gives us a quadratic equation in \(t\), which we can solve to find the intersection points.
The algorithm is as follows:
\[(\mathbf{o} + t\vec{d} - \mathbf{c})^2 - R^2 = 0\] \[(at^2 + bt + c) = 0\]Where:
\[a = \vec{d} \cdot \vec{d}\] \[b = 2(\mathbf{o} - \mathbf{c}) \cdot \vec{d}\] \[c = (\mathbf{o} - \mathbf{c}) \cdot (\mathbf{o} - \mathbf{c}) - R^2\] \[\Delta = b^2 - 4ac\] \[t = \frac{-b \pm \sqrt{\Delta}}{2a}\] \[t_{min} = \min(t_1, t_2)\] \[t_{max} = \max(t_1, t_2)\]This will let us determine the intersection time of the ray with the sphere, and we can check if the time falls within the interval \([t_{min}, t_{max}]\) and if so we update our ray’s \(t_{max}\) and save information about the intersection. And we can compute the normal at the intersection point by simply normalizing the vector from the sphere’s center to the intersection point.
Results
We can now render images with normal shading for a few small .dae files.




Bounding Volume Hierarchy
The Building Scene above took 161.1159s to render while others like the cube took under a second. The increase in time is due to the increased number of primitives in the scene.
[PathTracer] Input scene file: ../dae/keenan/building.dae
[PathTracer] Rendering using 8 threads
[PathTracer] Collecting primitives... Done! (0.0018 sec)
[PathTracer] Building BVH from 39506 primitives... Done! (0.0003 sec)
[PathTracer] Rendering... 100%! (161.1159s)
[PathTracer] BVH traced 1807017 rays.
[PathTracer] Average speed 0.0112 million rays per second.
[PathTracer] Averaged 8417.173796 intersection tests per ray.
[PathTracer] Saving to file: part1_building.png... Done!
As the number of primitives in a scene increases, the cost of ray intersection tests can become prohibitively expensive. Currently, we are testing every ray against every primitive in the scene, which results in a time complexity of \(O(n)\), where \(n\) is the number of primitives. To reduce this cost, we can use a Bounding Volume Hierarchy (BVH) to organize the primitives into a tree structure. This allows us to quickly discard large portions of the scene that do not intersect with the ray, reducing the number of intersection tests required, allowing us to achieve a time complexity of \(O(\log n)\).
Another example is our cow scene, which took 5.6 seconds to render without BVH acceleration:

[PathTracer] Input scene file: ../dae/meshedit/cow.dae
[PathTracer] Rendering using 8 threads
[PathTracer] Collecting primitives... Done! (0.0002 sec)
[PathTracer] Building BVH from 5856 primitives... Done! (0.0001 sec)
[PathTracer] Rendering... 100%! (5.6094s)
[PathTracer] BVH traced 473529 rays.
[PathTracer] Average speed 0.0844 million rays per second.
[PathTracer] Averaged 1134.760302 intersection tests per ray.
[PathTracer] Saving to file: cow.png... Done!
[PathTracer] Job completed.
Task 1
To create our Bounding Volume Hierarchy, we want to create a binary tree where each node represents a bounding box that encloses a set of primitives. We can do this recursively, starting with the root node that encloses all primitives in the scene and splitting the primitives according to a heuristic to create ‘left’ and ‘right’ child nodes. We continue this process until we reach a leaf node that contains a small number of primitives.
In my implementation, I first tried to split the primitives along the axis of greatest variance, using the average centroid of the primitives as my splitting point. When I computed the BVH on cow.dae, I had a tree a depth of 13. My next attempt was simpler, where I still chose to split along the axis of greatest variance, but I simply split the primitives in half. This resulted in a tree with a depth of 11.
We can visualize differences this heuristic makes by comparing the two trees:
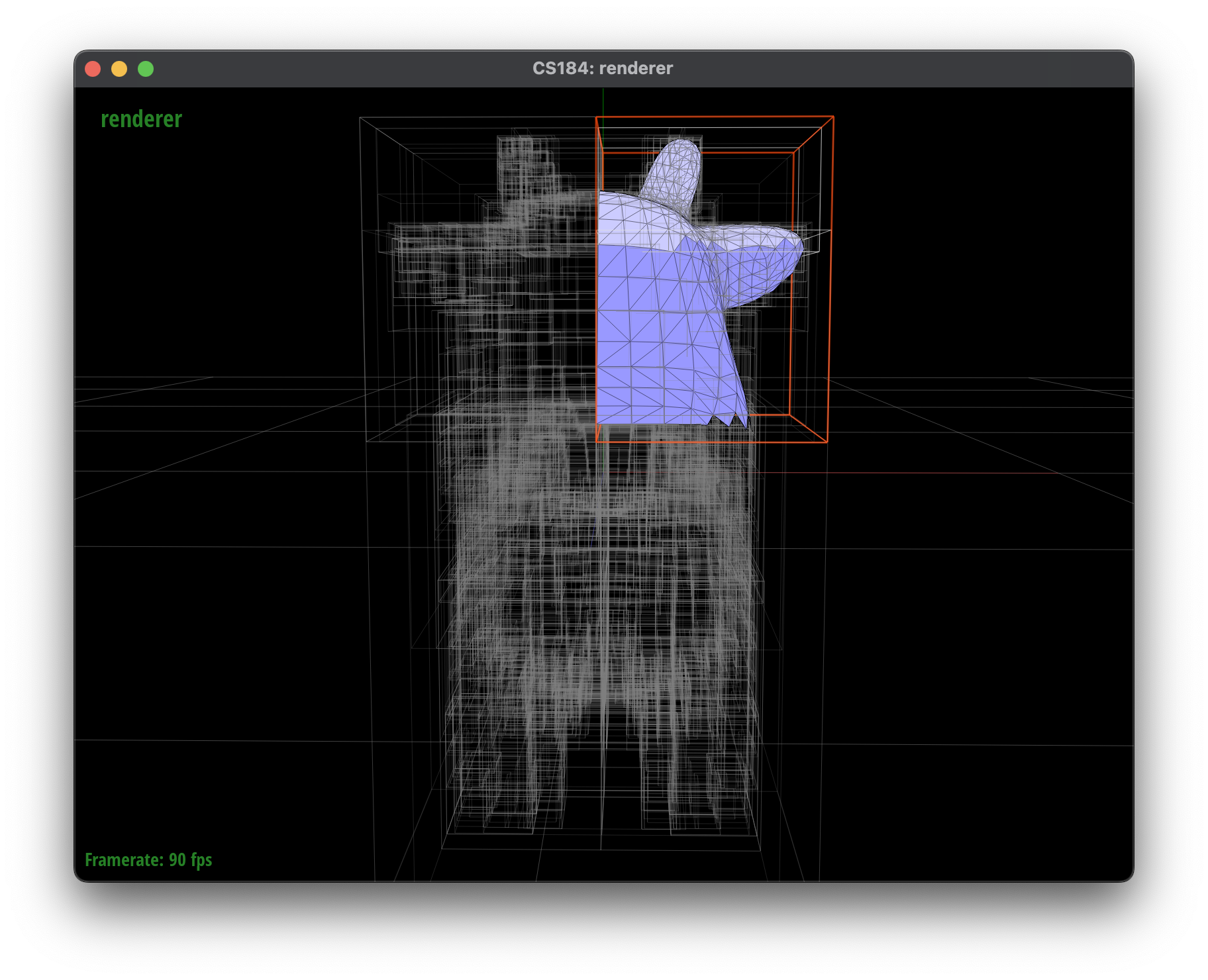
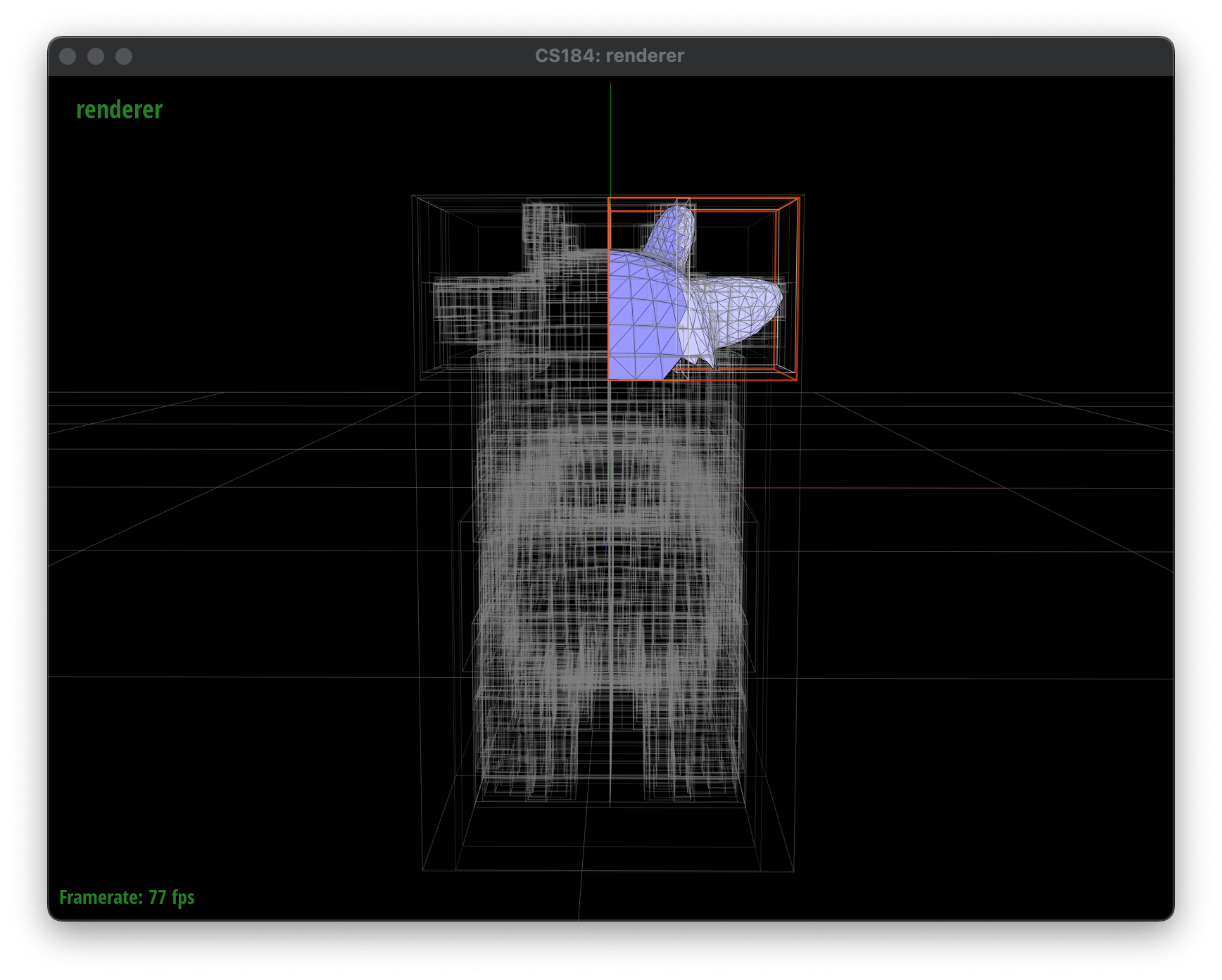
Since we want our BVH to be logarithmic in depth and log2(5856) ~ 12.5, we can say both are reasonable results. However, the half split BVH is more balanced and has a lower depth, which is generally better for performance.
I decided to implement a Surface Area Heuristic (SAH) to create a more efficient BVH structure. The SAH heuristic is based on the idea that we want to minimize the cost of traversing the BVH tree, which is a combination of the cost of intersecting the ray with the bounding box and the cost checking the ray against all primitives in each leaf node multiplied by the probability of hitting that leaf node. Therefore, the surface area of the bounding box gives us a good understanding of the probability of hitting that node, so minimizing the overall cost would involve minimizing the surface area of the bounding boxes of the left and right child nodes.
I relied on this textbook for a guide on how the SAH heuristic works and how to implement it in cpp. In my opinion, the assumption that the best axis to split along is the one with the greatest range is a good one, however I believe that variance is a better heuristic than range. This is because variance is a measure of how spread out the data is, and if the data is spread out, it is more likely that a split can be chosen that will separate the data into two distinct groups. This is important because in our SAH heuristic, we want to minimize the surface area of the bounding boxes of the left and right child nodes, and if the data is spread out, it is more likely that a split can be chosen that will separate the data into two distinct groups. I will continue to look into this to determine if my reasoning for using variance is correct.
After implementing the SAH heuristic, the depth of the tree was shockingly increased to 16. This is may be due to the fact that the SAH heuristic has more uneven splits as a result of the cost function, which can lead to a deeper tree. Overall the computation cost of a ray intersection test is reduced, while the traversal through the tree may have been increased. This is a tradeoff that is worth it in my opinion, as the cost of ray intersection tests is much higher than the cost of traversing the tree.
Let us take a look at the cow split using the SAH heuristic:
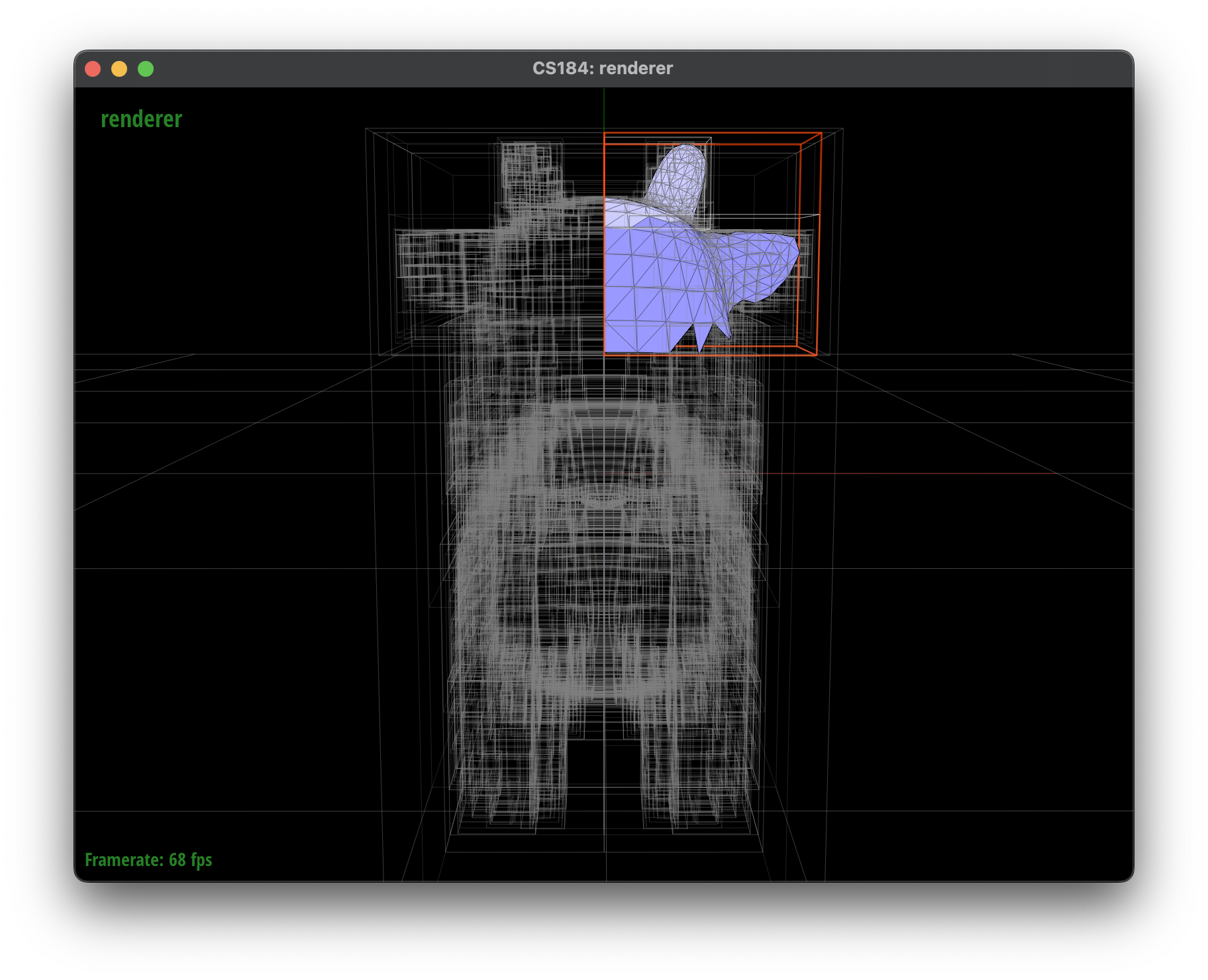
Task 2
Now we can implement the intersection test for our bounding boxes, this can be simplified for each of the 3 axes, where we check if the ray intersects the bounding box along the axis. We can update the time intervals that our ray intersects the bounding box, which will carry forward information.
Task 3
Now we can implement the BVH intersection test, where we traverse the BVH tree to find the closest intersection point. We start at the root node and check if the ray intersects the bounding box of the node. If it does, we check if the node is a leaf node, and if so we test the primitives in the leaf node. If the node is not a leaf node, we recursively test the left and right child nodes. Because our intersection tests update our ray’s time interval, we are left with the closest intersection point.
Results
We can now render images with normal shading for a few large .dae files that we can only render with BVH acceleration.
Cow Scene:
❯ ./pathtracer -t 8 -r 800 600 -f cow.png ../dae/meshedit/cow.dae
[PathTracer] Input scene file: ../dae/meshedit/cow.dae
[PathTracer] Rendering using 8 threads
[PathTracer] Collecting primitives... Done! (0.0003 sec)
[PathTracer] Building BVH from 5856 primitives... BVH Depth: 16
Done! (0.0023 sec)
[PathTracer] Rendering... 100%! (0.0388s)
[PathTracer] BVH traced 134568 rays.
[PathTracer] Average speed 3.4652 million rays per second.
[PathTracer] Averaged 4.076385 intersection tests per ray.
[PathTracer] Saving to file: cow.png... Done!
[PathTracer] Job completed.

Building Scene:
❯ ./pathtracer -t 8 ../dae/keenan/building.dae
[PathTracer] Input scene file: ../dae/keenan/building.dae
[PathTracer] Rendering using 8 threads
[PathTracer] Collecting primitives... Done! (0.0018 sec)
[PathTracer] Building BVH from 39506 primitives... BVH Depth: 21
Done! (0.0204 sec)
[PathTracer] Rendering... 100%! (0.1948s)
[PathTracer] BVH traced 696438 rays.
[PathTracer] Average speed 3.5746 million rays per second.
[PathTracer] Averaged 7.951282 intersection tests per ray.
[PathTracer] Rendering... 100%! (0.1962s)
[PathTracer] BVH traced 715852 rays.
[PathTracer] Average speed 3.6486 million rays per second.
[PathTracer] Averaged 7.963509 intersection tests per ray.

Lucy Scene:
❯ ./pathtracer -t 8 ../dae/sky/CBlucy.dae
[PathTracer] Input scene file: ../dae/sky/CBlucy.dae
[PathTracer] Rendering using 8 threads
[PathTracer] Collecting primitives... Done! (0.0074 sec)
[PathTracer] Building BVH from 133796 primitives... BVH Depth: 24
Done! (0.0862 sec)
[PathTracer] Rendering... 100%! (0.2072s)
[PathTracer] BVH traced 765431 rays.
[PathTracer] Average speed 3.6949 million rays per second.
[PathTracer] Averaged 3.609203 intersection tests per ray.
[PathTracer] Rendering... 100%! (0.2113s)
[PathTracer] BVH traced 893601 rays.
[PathTracer] Average speed 4.2295 million rays per second.
[PathTracer] Averaged 3.569567 intersection tests per ray.
[PathTracer] Saving to file: CBlucy_screenshot_3-18_3-55-31.png... Done!


Our cow scene went from 5.6 seconds to 0.0388 seconds, for an improvement of 144x. Our building scene went from 161.1159 seconds to 0.1948 seconds, for an improvement of 827x. It is clear that BVH acceleration makes a significant difference in rendering time for scenes with a large number of primitives, and we can see the average intersection tests per ray is significantly lower with BVH acceleration, decreasing by a factor of over 1000x in some cases. The time increase in building the BVH is clearly worth the time saved in rendering.
Direct Illumination
In our path tracer, we want to simulate the interaction of light with the scene, so we will need to get rid of our current implementation which uses the normal vector as a stand-in for the surface color. We will start by implementing direct illumination, which is the process of simulating the light that directly hits a surface. This involves calculating the light that comes from the light sources in the scene and hits the surface directly, without any bounces.
Task 1
We will start by updating our BSDF (Bidirectional Scattering Distribution Function) class to handle the reflection of light on diffuse surfaces. Our function DiffuseBSDF::f takes in wo and wi as the outgoing and incoming directions of the light in the object space, and returns the color of the light that is reflected in the direction wi. Because we are simulating a diffuse surface, the incoming and outgoing directions and point of intersection have no effect on the reflected light, so we can simply normalize the albedo of the surface by dividing by \(\pi\).
Task 2
Next, we will begin to implement our zero-bounce illumination by modifying PathTracer::zero_bounce_radiance to have the rays return the emmission of their first intersection. This will visualize where the light is coming from in the scene, but will not account for any bounces of light.

Task 3
Next we will our one-bounce lighting, starting with Uniform Hemisphere Sampling which is a method of sampling the hemisphere around a intersection point. This is useful for simulating the reflection of light on a surface, as it allows us to sample the directions that light can come from in a way that is unbiased. We will modify PathTracer::estimate_direct_lighting_hemisphere to use this sampling method to estimate the direct lighting at a point. The algorithm involves using a Monte Carlo estimator to sample the hemisphere around the point and calculate the average light that comes from the light sources in the scene. This will give us a more accurate estimate of the direct lighting at the point, however it requires a large amount of samples to converge to the correct value. We can visualize the difference between the two methods by comparing the noise levels in the soft shadows of a scene with an area light source.


Task 4
However we can be smarter about where we sample, after all we know that in our first bounce, the light must come from the light sources in the scene. Therefore we can modify PathTracer::estimate_direct_lighting_importance to instead sample from the points of intersection towards each of the light sources in the scene. If the ray intersects with an object on the way to the light source, we can ignore the light source as it is occluded. Otherwise, given we account for the range slightly above the surface and before the lightsource, a lack of a ray intersection between the two points means the lightsource is visible. If we have a point light source, we need to only sample it once, however if we have an area light source, we need to sample it multiple times to account for the area of the light source. By summing the light from each of the light sources, we can estimate the lighting reflected to the camera at that point. With this, we can achieve a more accurate estimate of the direct lighting at a point because we aren’t metaphorically/actually shooting in the dark in the hopes of hitting a light source.


Results
Let us take a look at what happens when we increase the number of source light rays in our importance sampling, while holding the number of samples per ray constant.




As we increase the number of samples for each source light ray in our importance sampling, we can see the shadows becoming softer, this is because more of them are being sampled, and instead of having a very poor estimate of the light, the Monte Carlo estimator is able to converge to the correct value. This is why we see the noise levels decrease as we increase the number of samples. However, so does the time it takes to render the image, as we are sampling more rays for each light source.
❯ ./pathtracer -t 8 -s 1 -l 1 -m 6 -f part3_importance_sampling_s1_l1.png -r 480 360 ../dae/sky/CBbunny.dae
...
[PathTracer] Rendering... 100%! (0.0411s)
...
❯ ./pathtracer -t 8 -s 1 -l 4 -m 6 -f part3_importance_sampling_s1_l4.png -r 480 360 ../dae/sky/CBbunny.dae
...
[PathTracer] Rendering... 100%! (0.1143s)
...
❯ ./pathtracer -t 8 -s 1 -l 16 -m 6 -f part3_importance_sampling_s1_l16.png -r 480 360 ../dae/sky/CBbunny.dae
...
[PathTracer] Rendering... 100%! (0.3653s)
...
❯ ./pathtracer -t 8 -s 1 -l 64 -m 6 -f part3_importance_sampling_s1_l64.png -r 480 360 ../dae/sky/CBbunny.dae
...
[PathTracer] Rendering... 100%! (1.0336s)
...










As we can compare, importance sampling is able to achieve a much better estimate of the direct lighting at a point than uniform hemisphere sampling for the same number of samples. This is because importance sampling is able to sample the areas on the hemisphere that are possible to contribute to the lighting in one bounce, while uniform hemisphere sampling’s random sampling can miss these possibly small areas in soft shadows. We can that the noise level is lower in the importance sampling images, and the shadows are softer, which is a sign that the Monte Carlo estimator is converging to the correct value. Additionally, there are time savings because we can discard rays that intersect with objects on the way to the light source, which is not possible with uniform hemisphere sampling as we need to always find the closest intersection point. After writing this section, I was able to go back to my importance sampling implementation and use the has_intersection function of the BVH to check if the ray intersects with an object on the way to the light source, which is a much more efficient way of checking if the light source is visible rather than getting the closest intersection point.
Global Illumination
With our current implementation, we are only able to simulate the direct lighting in the scene, which is the light that comes from the light sources and hits the surface directly, or the light that is reflected off the surface in one bounce. However, we want to simulate the indirect lighting in the scene, which is the light that comes from the light sources, bounces off multiple surfaces, and eventually hits the surface. This is important because it is the light that gives the scene its color and makes it look realistic.
Task 1
We will re-examine our function sample_f in our BSDF class, which is used to sample an incoming direction wi given an outgoing direction wo using a cosine-weighted hemisphere. We store the pdf of the direction in pdf, which is the probability of sampling the direction wi given the direction wo, and return the reflectance of the surface by using DiffuseBSDF::f. This is be important for our next task, in which we will want to sample outgoing rays from our hit points.
Task 2
In this section, we complete the function PathTracer::at_least_one_bounce_radiance, which will help us simulate the indirect lighting in the scene. We begin by modifying the initialization of our rays to have a depth of max_ray_depth, which is the maximum number of bounces we want to simulate. Our algorithmic logic is as follows:
- If our ray has reached the maximum depth i.e.
max_ray_depthis 0, we return the one-bounce radiance at the hit point. - Else, we sample the incoming direction
wiusing the BSDF at the hit point. - If this ray intersects with an object in the scene, we recursively call
at_least_one_bounce_radiancewith the new ray and decrement the depth. - If isAccumBounces is true, we accumulate the radiance from one-bounce at our hit point with the radiance from the recursive call.
- We return the radiance at the hit point.
Task 3
We will now modify our function PathTracer::at_least_one_bounce_radiance to simulate the integration over all possible path lengths in the scene. We will accomplish this by applying a Russian Roulette technique, which is a method of randomly terminating rays before they have reached the maximum depth. This is done by using a probability of termination, which I have set to 0.35. This will allow us to increase the maximum depth of our rays without increasing the render time significantly, as rays have 35% chance of being terminated at each bounce. In fact, at a depth of 16, a ray only has a 0.1 % chance of reaching the maximum depth.
Results
Lets take a look at the results of our global illumination implementation vs. their direct illumination counterparts.








We can see that the indirect illumination images have a much more realistic look to them, as they are able to capture the color of the scene and the light that is reflected off the surfaces. This is because the indirect illumination is able to simulate the light that bounces off multiple surfaces and eventually hits the surface, which is what gives the scene its color. The direct illumination images are much more flat and do not capture the color of the scene, as they only simulate the light that comes from the light sources and hits the surface directly or is reflected off the surface in one bounce.
However, not all scenes equally benefit from indirect lighting, let us take a look at a scene that is significantly more complex than the others, but doesn’t have the geometry that would benefit from indirect lighting.



To understand the effect that indirect lighting has, let us see exactly what it is adding by removing the first bounce contribution in our indirect illumination image.



We can see that the indirect illumination image without our ray’s first intersection’s one-bounce contribution is much darker and has less color than the indirect illumination image with this contribution. This is because this first one-bounce calculation captures the light that comes from this surface directly from the light sources, which carries significant energy that is used in our scene coloring. You can also visualize how the two images on the left would combine to form the right image.
Next, we will compare the quality of the rendered image with different numbers of bounces of light. We will render the mth bounce of light with max_ray_depth set to 0, 1, 2, 3, 4, and 5, and isAccumBounces=false. We will also compare the rendered views of accumulated and unaccumulated bounces for the bunny scene with max_ray_depth set to 0, 1, 2, 3, 4, and 5. We will remove our zero-bounce contribution from our non-accumulated bounces images to see just the effect of the bounces of light.












We can see that the accumulated bounces images gain brightness and color all around, but most noticeable in the shadows in our early increases. This is because the accumulated bounces are able to capture the light that bounces off multiple surfaces and eventually hits the surface. The brightness of each incremental bounce is less than the previous one, however we can see distinct information in each bounce, such as the 2nd bounce containing information to the bottom areas of the bunny, which is being generated from bounces that have gone off the floor and then reached the light. This is contrasted to the third bounce, which lacks this shadow information, but upon inspection contains more information around the creases of the bunny, which is being generated from bounces that have escaped crevices and then reached the light. This is a significant improvement over our direct illumination images, which are much flatter and this expected behavior of light.
Now we can compare the effect of Russian Roulette on the quality of the rendered image. We will output the Russian Roulette rendering with max_ray_depth set to 0, 1, 2, 3, 4, and 100. Normally, 100 bounces would be computationally expensive, but because of Russian Roulette, we can still get a good estimate of the image with a much lower number of bounces.






We can see that the Russian Roulette from 1 to 4 bounces offers a significant improvement in the quality of the image, as we have a larger range of path lengths we sample from. However, the Russian Roulette with 100 bounces does not offer a significant improvement in the quality of the image, as we do not even likely reach the maximum depth of 100 bounces. This is because the probability of a ray reaching depth \(d\) is \((1 - p*{term})^d\), where \(p*{term}\) is the probability of termination, which is 0.35 in our case. This means that the probability of a ray reaching depth 100 is \(1.95585054 \times 10^{-19}\), which is very low.
Finally, we will compare the effect of the number of samples per pixel on the quality of the rendered image. We will render the dragon scene with 4 light rays and compare the rendered views with various sample-per-pixel rates: 1, 2, 4, 8, 16, 64, 256, and 1024.








We can see that the quality of the rendered image improves as we increase the number of samples per pixel. This is because the more samples we take per pixel, the more accurate our estimate of the radiance at that pixel will be. This is because in our Monte Carlo estimation, we need many samples to be able to obtain a good average, which will give us a more accurate estimate of the radiance at that pixel. We can see that the images with 1 and 2 samples per pixel have a lot of noise in them, while the images with 1024 samples per pixel are much cleaner and have less noise.
Adaptive Sampling
It is quite computationally expensive to have 1024 samples across the entire scene, as certain parts of the scene may not need that many samples to get a good estimate of the radiance at that pixel, while other parts of the scene will definitely require the full 1024 samples. This is where adaptive sampling comes in, with it we can take more samples in the areas of the scene that need it and fewer samples in the areas of the scene that do not need it. This will allow us to get a good estimate of the radiance at each pixel in the scene while reducing the number of samples we need to take.
Task 1
We will go back to our PathTracer::raytrace_pixel function to implement adaptive sampling. We will begin by initializing variables to keep track of the current number of ray samples per pixel, the sum of illuminance received from every ray sample, and the sum of the illuminance squared received from every ray sample. As we loop through the number of samples per pixel, as before, we will calculate the radiance at the pixel for each sample and add it’s contribution onto a running sum. Then for each ray sample, we will add to our two running luminance sums, and when we have reached our batch size, we will calculate the mean, \(\mu\), and the variance, \(\sigma^2\), of the luminance samples. We will then calculate the confidence interval, \(I\), of the luminance samples, which is given by \(I = 1.96 \times \frac{\sigma}{\sqrt{N}}\), where $ N $ is the number of samples. If the confidence interval is less than \({tol} \times \mu\), we will break out of the loop and return the mean of the radiance sum. If the confidence interval is greater than \({tol} \times \mu\), we will continue to take samples until we reach the maximum number of samples per pixel.
Results
I first tested out adaptive sampling on the bunny scene with 2048 samples per pixel, 1 light ray, a maximum depth of 5, with a batch size of 64 and a tolerance of 0.05. This took 108.3176s to render!


I additionally tested out adaptive sampling on the dragon scene with the same parameters as the bunny scene, which took 221.1808s to render. (There were other large renders running concurrently, so this time is not indicative of the actual time it would take to render the scene.)

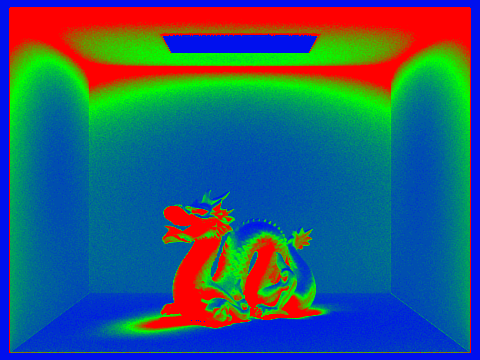
I decided to go for two large 1080x1080 renders to see all the implemented features in action.



